CALCULS DIMENSIONNEL

  
Problème de l'injection

Avant de calculer la roue il faut choisir la largeur d'injection comme vu à la page précédente

Le réglage du débit ,ci dessus , est assez rustique    

Dans celle de droite  , l'eau est entraînée par suite de la directrice unique dans un mouvement circulaire ou l'angle est à peu près respecté
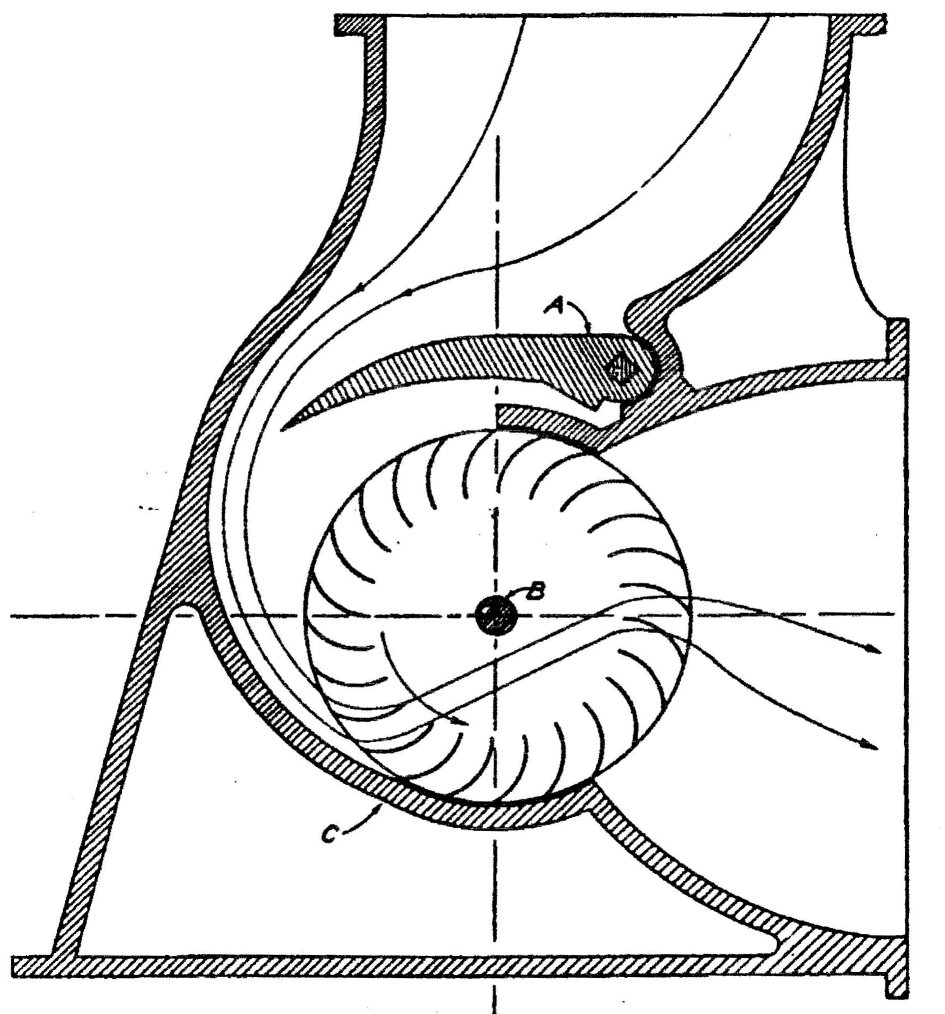
La largeur active telle que vue sur le dessin et pour l'ouverture considérée est d'environ 2 aubes.
Quand la directrice offre l'ouverture maximale , les filets d'eau sont injectés sur environ 6 aubes simultanément
Cet injecteur est hydrauliquement bien etudié

Comme la largeur dépend du nombre d'aubes , les constructeurs parlent souvent d'un angle d'admission en degrés lequel est indépendant de ce nombre .

Une autre image provient d'une note de calcul d'un pays d'Europe de l'Est


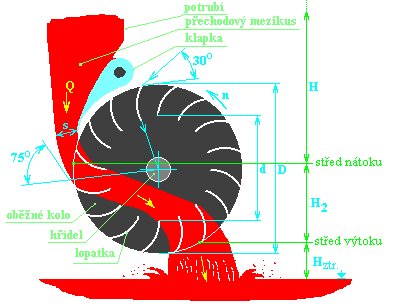
Cette note serait très intéressante s'il n'y avait le problème de la langue
remarquons encore que cette roue est du type injecteur assez rudimentaire il équivaut à un injecteur rectangulaire avec admission de faible épaisseur

C'est la solution qui a été adoptée dans l"étude du fichier Banki.pdf

Pour les grandes admissions comme déjà dit il faut un injecteur bien profilé pour que tous les filets attaquent le cercle externe sous l'angle d'attaque en principe de 16 degrés

Dimensionnement (méthode classique)

Ces calculs issus de formules pré-établies donnent rapidement les dimensions principales d'une roue.
le symbole sqr désigne la racine carrée
le symbole * désigne la multiplication
Diamètre et largeur
Soient :
H la hauteur de chute en mètres
Q le débit en m3/sec
h le rendement présupposé
a l'angle d'attaque en degrés (16 à 22 environ)
L la largeur du jet (souvent celle de la roue)
lambda  angle d'interception du jet ( entre 45 et  120 degrés selon les injecteurs) , en radians
Le jet de vitesse V =Sqr(2 * g * H) à 2% près attaque la circonférence externe sous l'angle alpha
Son épaisseur e ( en m) est telle que :

Q = V * e *L
L*e=Q/V

et son interception t  sur la circonférence est telle que :
t =e/sin( a)
et ausi : t= D* lambda / 2
éliminant t
DL = 2* e * L /V*( lambda *sin( a))


DL = 2* Q / (V * lambda *sin( a))

Dapproché  = sqr(DL)
Dapproché  est une valeur approchée du diamètre , telle que diamètre = largeur
On choisira une valeur D définitive ,le produir DL ne changeant pas

D et L sont en mètres

Dans les tracés modernes lambda est voisin de 90 degrés
Exemple:

H= 3m   d'ou V = 7.67 m/s

a =20 degrés   , sin( a )=0.34
lamda=90 degrés  soit pi/2
Q=1 m3/s

On trouve facilement
DL= 0.485

Si D= L alors D= 0.7

Attention dans certains manuels on trouve une formule empirique  du genre
DL =  Q / racine(H)  qui conduit à une roue environ 2 fois trop petite !!

On trouve aussi sur le web des sites qui se veulent sérieux et qui sont incapables de fournir une formule correcte

Diamètre et Largeur
La formule précédente permet de choir D ou l et d'en déduire l'autre dimension
Souvent on prend D < L , alors la roue tourne plus vite

Certaines roues ont de plus grandes largeurs avec division en 1/3  2/3 ce qui permet de turbiner des débits de valeur relative 1 , 2 , 3 à plein réglage
Il faut évidemment que l'injecteur soit cloisonné en conséquence

Vitesse de rotation

N = 38 * sqr(H) / D  en T/min

Le cercle intérieur a un diamètre entre 0.55 à 0.66 D
Le nombre d'aubes doit être tel que l'épaisseur du jet soit un peu inférieure à l'écartement entre les aubes.
Dans ces conditions une seule aube est censée active à la fois 
Le problème à régler est qu'il n'y ait pas d'eau perdue par engorgement.

Tracé des aubes
Ce tracé est d'une assez grande simplicité.
Cependant il faut savoir que les formules ci après ont été obtenues par des calculs un peu plus laborieux que nous éviterons au lecteur .
Ceux qui s'y intéresseraient pourraient visiter le site et récupérer un gros fichier pdf (Acrobat) qui est en anglais avec les unités anglaises .

http://home.carolina.rr.com/unclejoe
Il semble que ce site ait disparu du Web (Juin  2003) Me demander le fichier si souhaté

Les aubes sont obtenues par des arcs de cercle dont le rayon est 
égal à 0.326 * R1    (R1=D/2).

Les centres K de ces cercles sont eux même sur un cercle de rayon 0.736 * R1























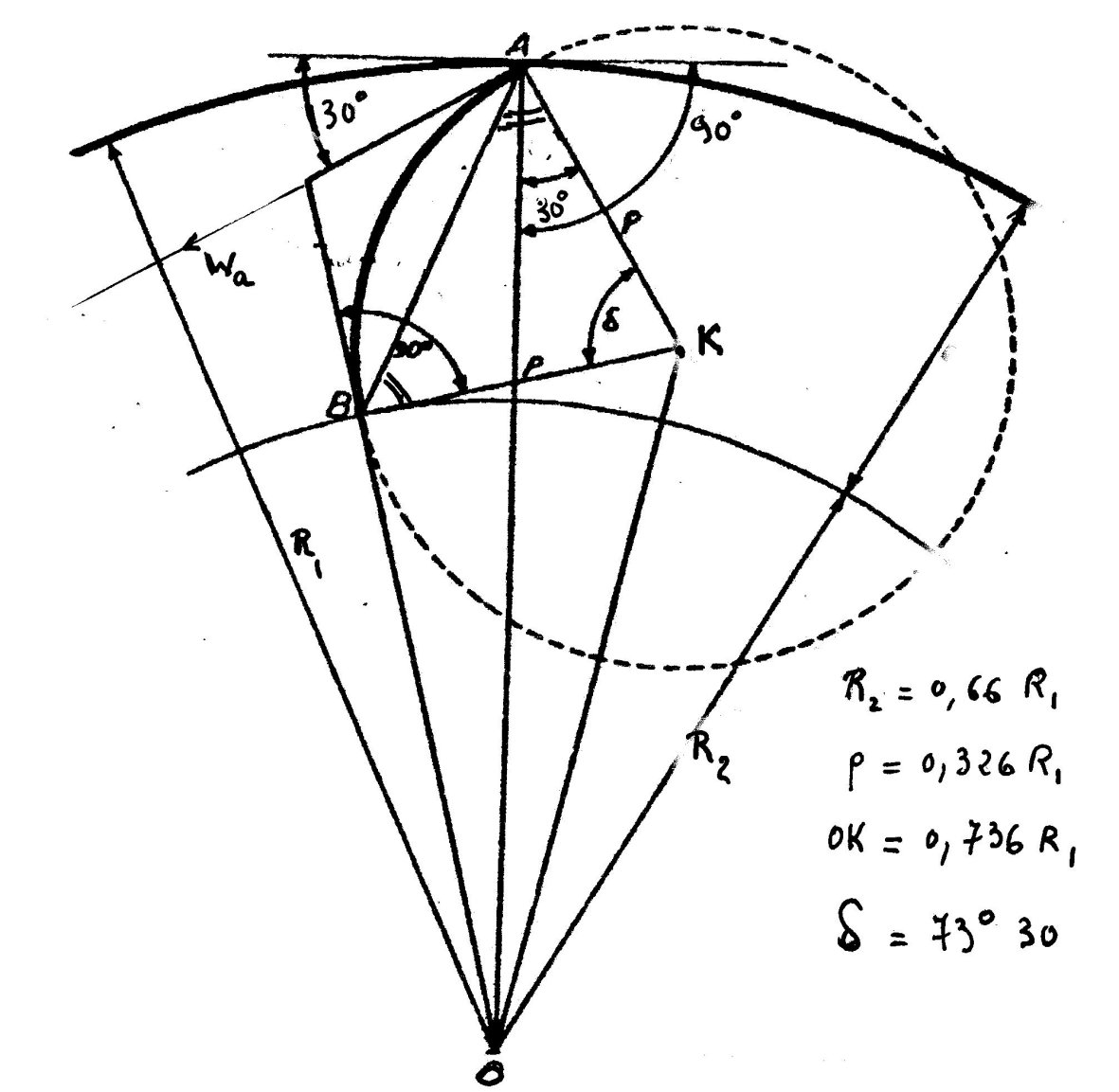
Le graphique ci dessus nous indique comment placer une aube.

CONSTRUCTION
Contrairement aux autres turbines dont la constructions est quasiment irréalisable par l'amateur , sauf à faire des approximations qui détruisent le rendement,  la turbine Banki , pour de petites puissances notamment , est relativement facile à  réaliser .

Aubes
Les aubes en effet n'ont pas de surfaces gauches comme les Francis par exemple qui sont les plus difficiles  à réaliser sur le plan du tracé.
Beaucoup utilisent des tubes en plastique dans lesquels ils découpent les aubes et certains visiteurs m'ont dit avoir réalisé la bâche en contreplaqué "marine" d'épaisseur suffisante et ceci pour des puissances de quelques Kw.
Cependant il faut savoir que les aubes sont soumis à des efforts assez grands et qu'une fixation insuffisante peut entraîner l'éclatement de la roue

Les dessins de haut de la  page  donnent des solutions pour la réalisation de l'injecteur 
La largeur de l'injecteur sera généralement un peu inférieure à celle de la roue , pour éviter les pertes d'eau .

Méthode de l'Université de Clemson (USA)

Cette méthode est actuellement reconnue comme l'une des meilleures par ceux qui cherchent à construire leur propre turbine

Le fichier Banki.pdf , bien connu ,(travaux de  Mockmore and Merryfieldest  , Université de OREGON USA , 1949) , actuellement considéré comme inadéquat (erreurs de calcul , roue de rendement médiocre)

Voir au besoin A propos de la roue du fichier Banki.pdf

Dans cette méthode plus récente  (travaux de Nadim M.Aziz ) les paramètres sont modifiés : angle d'attaque  plus grand (22 degrés) , le rapport des cercles est un peu modifié, le tracé des aubes est obtenu après un calcul par un logiciel qui est fourni sous forme de feuille de calcul Excel dont l'emploi est assez simple.
Ce logiciel est disponible sur le site ci dessous (en fin de page  , le fichier Excel  peut être rapidement lancé et sauvegardé)

http://www.bluemountainavionics.com/greg/scpl.html

La version que je possède est le résultat d'un travail complémentaire pour faire apparaître les résultats en unités métriques mais je ne me sens pas autorisé à la diffuser

Cette méthode a été incorporée dans mon calcul des roues banki et dans mon logiciel  et dans l'option Calcul USA
Il n'est pas possible de donner ici le développement de ce  calcul
La valeur choisie pour le rapport des diamètres est 0.6 et non 0.66

il reste à faire  un choix pour la forme de l'injecteur ,le dessin de droite donne la solution  proposée par l'université de Clemson
Pour  le contrôle du débit ,  la forme de la directrice qui doit se loger dans ce volume n'est pas proposée par Clemson
En effet cet injecteur ouvert laisserait passer dans la gorge (S1) un débit d'eau trop important
(plus de 2 fois le débit nominal )

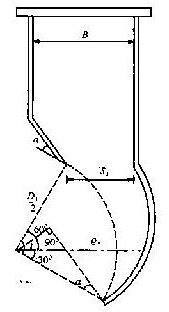
Cette forme de la directrice doit avoir un profil hydrodynamique convenable , afin de ne pas créer de pertes de charge
La directrice en haut et à droite dans cette page correspond à ces conditions
Ceci dit il y a bien des solutions possibles

 Le graphique ci dessous donne la méthode pour déterminer les aubes à partir des résultats du calcul



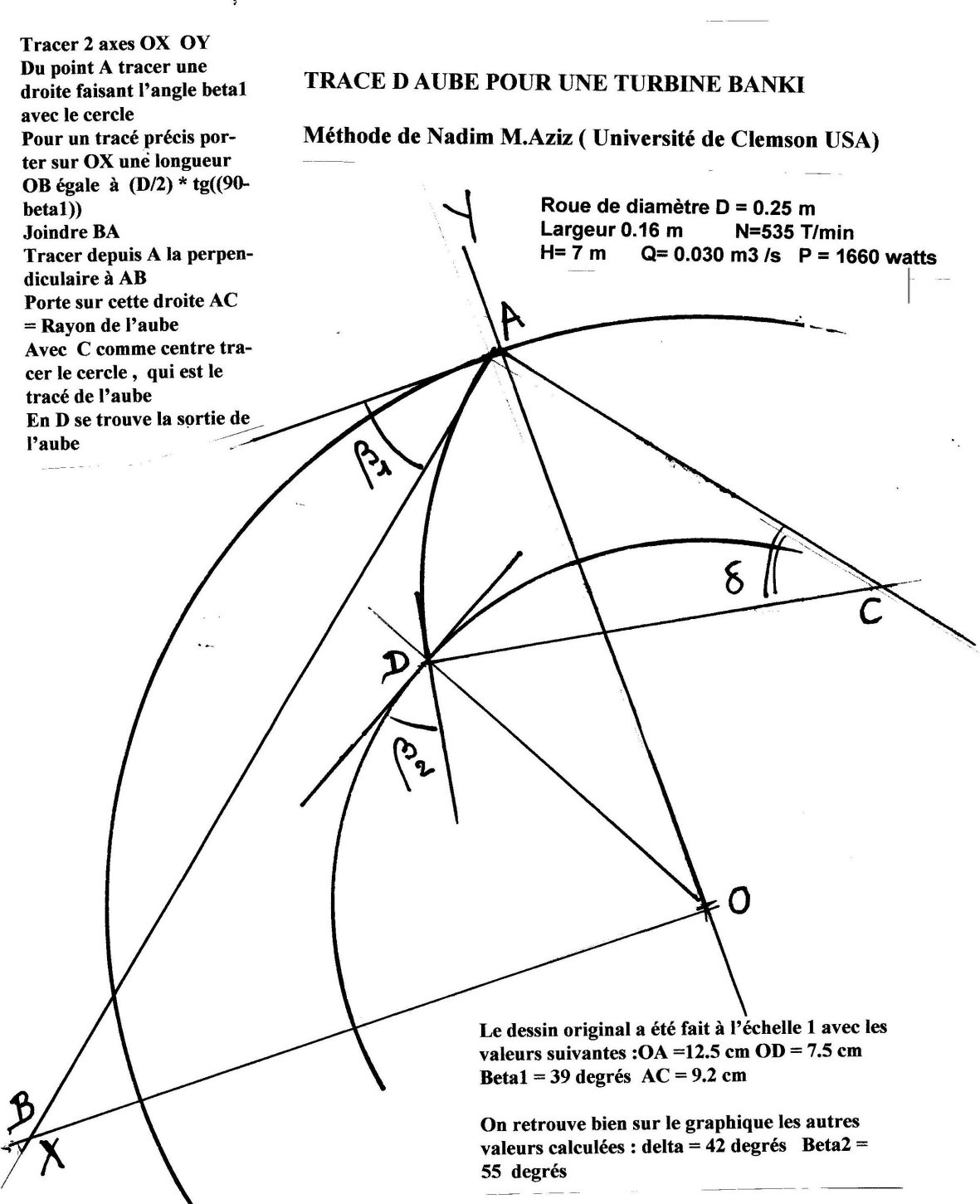
Disons enfin que la méthode USA propose une largeur de roue qui est 1.5 fois celle de l'injecteur

Vue partielle d'une petite turbine démontée (Constructeur WILLOT Belgique)



Le nombre d'aubes est de 30 environ , ce nombre n'est pas hyper critique

La valeur de lambda est de 90 degrés

Le rendement d'une roue établie sur ces bases peut avoir une valeur  très élevée

Le même projet réalisé avec le calcul classique donne pour le même diamètre et sensiblement la même vitesse de rotation une largeur de roue plus de 2 fois supérieure

> http://homepages.enterprise.net/hugh0piggott/

Retour page d'accueil