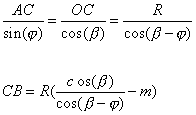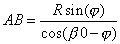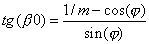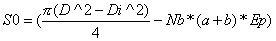CONSTRUCTION DE LA ROUE AU DESSUS
Généralités
Comme nous le verrons par le calcul , la difficulté de
réalisation d'une roue résulte des conditions suivantes , certaines étant
contradictoires
Emmagasiner un grand volume dans l'auget
Dessiner ce dernier pour qu'il se vide le plus tard possible
Tourner vite
Cette étude concerne principalement la roue au dessus avec aubes en
bois en 2 pièces pour 1 auget
L 'aube la plus proche du centre est dans l'alignement du rayon qui détermine
l'origine de l'auget suivant
Cependant le calcul sera étendu à une roue à aubes courbes
On désigne par
H la hauteur de chute géométrique en m
Q le débit nominal en l/s
D le diamètre extérieur de la roue hors tout
Di le diamètre intérieur (extérieur de la fonçure)
m = Di / D
j angle au centre séparant 2 augets
Nb nombre d'augets
N vitesse de rotation en T/min
a angle
d'entrée de l'eau
b angle
de l'aube avec le cercle externe
Ep épaisseur des aubes
Va vitesse d'entrée de l'eau
Kve coefficient de vitesse périphérique en % de Va (entre 0.4 et 0.8)
Les relations dans le triangle des vitesses donnent
et 
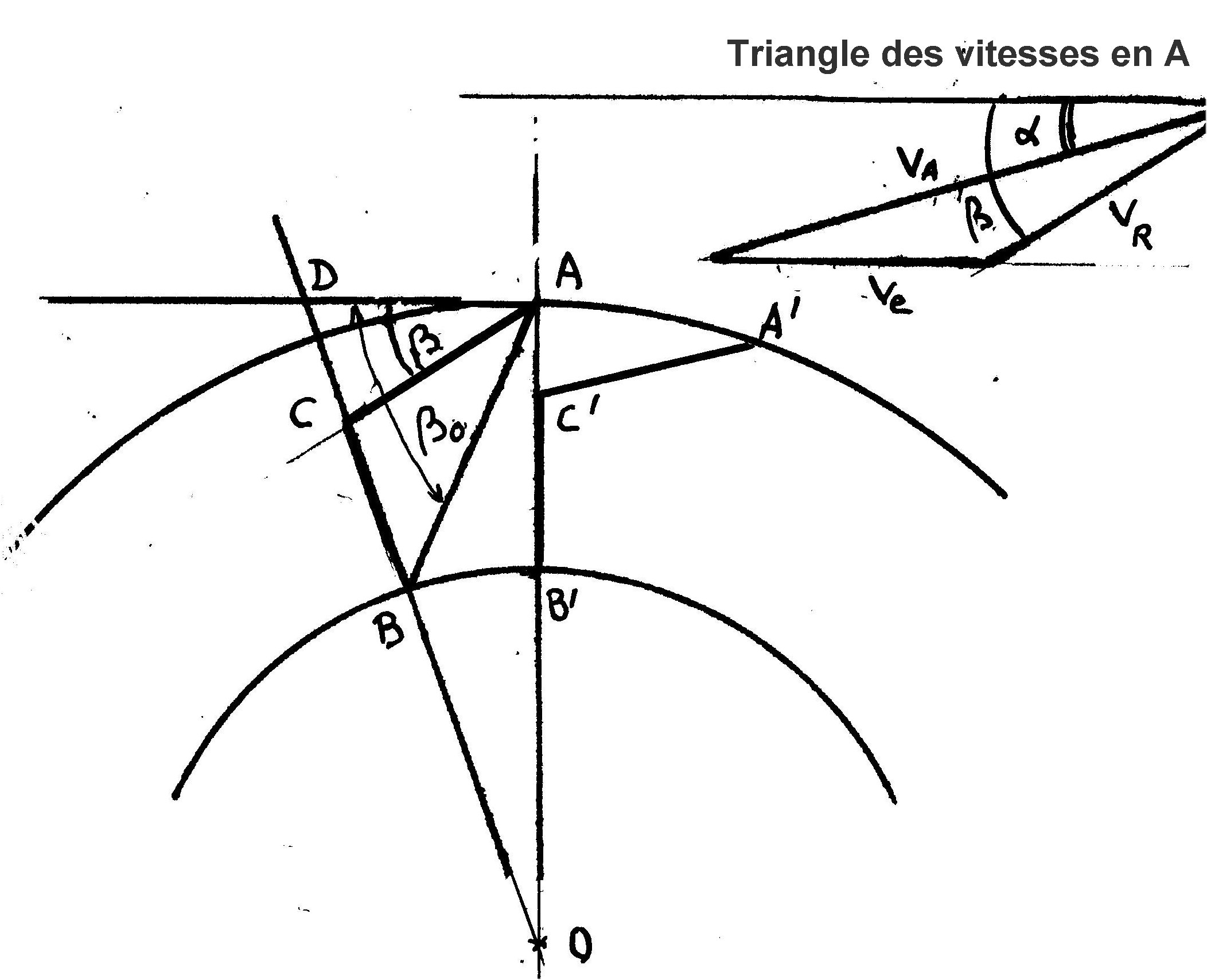
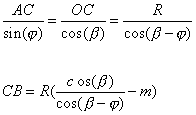
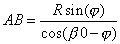
L'angle b0
étant déterminé par
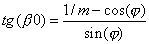
Ces éléments définissent complètement la géométrie
Posons :
AB =c CB =a AB = c
La surface du triangle ABC sera avec p = (a + b + c) / 2
(demi périmètre)
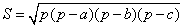
La surface utile de la couronne épaisseurs déduites est :
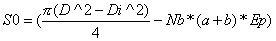
et pour 1 auget
Sa = S0 / Nb
Vidage anticipé
En l'absence de coursier inférieur et avec la
disposition d'aubes choisie l'eau commence à se vider lorsque la ligne AB passe
à l'horizontale
Si l'auget est empli selon cette surface , la ligne de premier déversement anticipé
sera la droite AB
En partant du point A au sommet de la roue , il faudra tourner d'un angle de180
°- b0 pour
que le coté AB soit horizontal , entraînant le commencement du vidage
indésirable
Rien n'interdit de dépasser ce taux de
remplissage mais plus
l'auget sera rempli plus la ligne de déversement sera
plus haute et le rendement diminué
Le vidage est fini lorsque la ligne AC passe à son tour à l'horizontale coresponsable
à une rotation p-b
L'image ci dessous , extraite d'un
Atlas par Armengaud (1) donne une meilleure visualisation du
problème
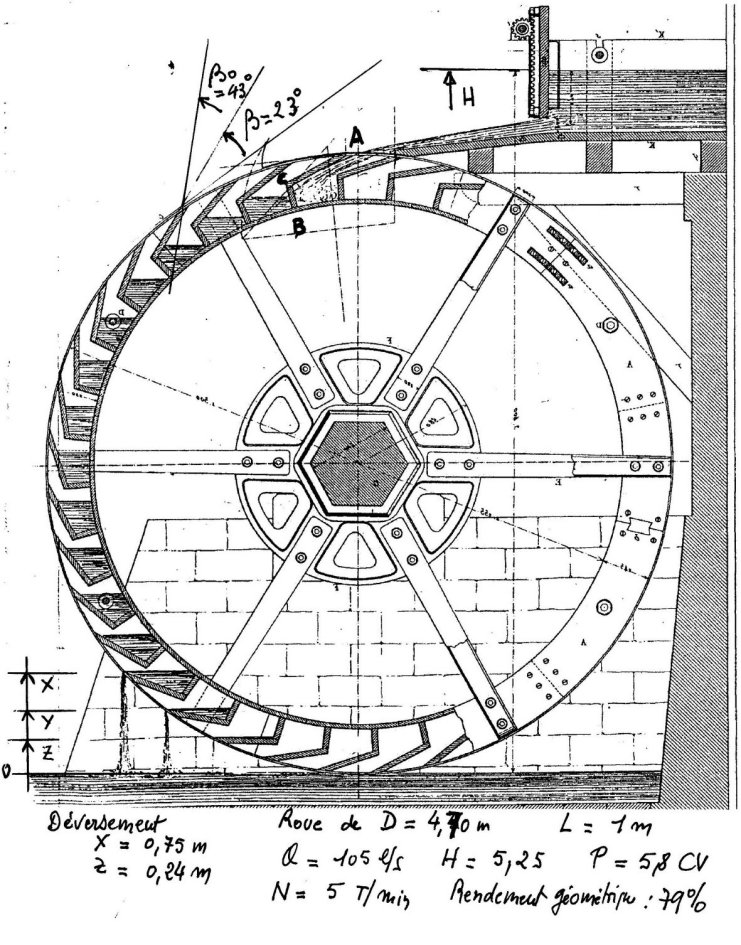
Les données numériques non connues car je ne possède qu'une partie de cet
ouvrage ancien ont été imaginées de façon vraisemblable et contrôlées
par le calcul( logiciel) . Le tracé donné par ce dernier est strictement
conforme au dessin et les angles b
et b0
ont été retrouvés avec une excellente précision mais il a fallu prendre
a petit
(14°) et la vitesse périphérique à seulement 0.5 V
Remarquer que l'angle a du
dessin est un peu inférieur à 14° et cette valeur est insuffisante
La largeur est sans objet mais varie avec le débit . Ici on a pris 1 m et
le débit (105 l / s /m) 'est faible mais la roue est du type à grand rendement
(79%) , la couronne est petite , la vitesse périphérique peu importante
Pour revenir au déversement , on admettra sans erreur notable que tout se passe
comme si la roue perdait la totalité de son eau lorsque le point A passe à la
cote Y , soit Y = Z + (X-Z) / 2
On calcule facilement :
X= 0.5 D (1-cos( b))
Z = 0.5 D (1-cos(
b0))
Ces valeurs sont très théoriques
En fait , on remplit davantage l'auget (jusqu'à 50%)
La ligne de premier déversement est donc décalée d'un angle supplémentaire
Influence du nombre des augets et autres
facteurs
On pourrait croire que le choix de ce nombre
est purement une affaire de .... goût
Il n'en est rien
Modifier ce nombre modifie le tracé des parois
En bref , diminuer les augets en nombre augmente leur longueur
De plus, le jet d'eau du débit maximum doit
pénétrer dans la roue avec une épaisseur qui ne dépasse pas l'écartement
entre augets
Comme l'angle b joue
un rôle impérieux dans le calcul , on est souvent obligé d'augmenter la hauteur
de la couronne pour avoir un tracé satisfaisant.
La vitesse d'entraînement joue aussi considérablement
Pour avoir b petit
, ce que l'on souhaiterait souvent , il faut une vitesse d'entraînement faible
, ce qui est souvent peu satisfaisant si on veut entraîner des récepteurs
rapides
Coursier supérieur et pénétration de l'eau
Nous revenons un peu en arrière pour nous
occuper du coursier supérieur
Une certaine partie h de la hauteur de chute est comme nous l'avons dit
"sacrifiée" pour mettre l'eau en vitesse
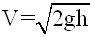 m/s m
m/s m
sans tenir compte de la perte de charge du
coursier
En prenant un coefficient moyen de 0.55 pour
le rapport entre V et la vitesse périphérique de la roue, on trouve facilement
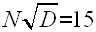 env.
env.

Le coursier a son point de départ au bas de la vanne
Il doit présenter une certaine pente pour éviter un ressaut et ceci en
fonction du nombre de Froude
De toute façon la pente est nécessaire pour ne perdre sur la vitesse de l'eau
, c'eat à dire compenser au moins la pertes de charge due au coursier
Pour cette dernière raison , la longueur du
coursier sera faible ( 0.5 à 1 m)
Respect de alpha
Pour respecter l'angle alpha d'intersection du
jet avec le cercle , la pente du coursier est généralement insuffisante
A pârtir de la fin du coursier , l'eau tombe
en jet libre
Il faut déterminer la parabole du jet ; nous considérerons le jet inférieur
Cette parabole est le trajet d'un corps lancé
dans le champ de gravité avec une vitesse initiale dont les composantes
horizontale et verticale sont connues
Si ce calcul assez simple semble rébarbatif ,
le lecteur pourra utiliser mon logiciel en pensant à initialiser l'échelle
graphique
Les aubes droites ont un angle vif et la
hauteur de passage de l'eau résultant de certains calculs peut être
insuffisante vu l'écueil du à ce point .
Dans le dessin du haut de cette page , la
hauteur de passage est approximativement AC' cos (b
)
Le logiciel vérifie cette condition avec une
marge de sécurité actuellement paramétrée à 20% : il faut en effet que la roue puisse récupérer
rapidement sa vitesse dans le cas de baisse anormale et que cette phase ne soit
pas simultanée avec une perte d'eau : il faut penser que le calcul est fait
pour le débit nominal et la vitesse nominale et que les condition temporaires
ne doivent pas être défavorisées.
L'emploi d'aubes courbes élimine pratiquement ce problème
Cas des aubes courbes
La plupart des dessins d'aubes courbes que
l'on trouve dans les manuels anciens figurent des aubes dont l'angle
b est
petit
La petitesse de b n'est
pas sans inconvénients : il faut pour un
a donné
réduire la vitesse périphérique , et si le rendement a plutôt tendance
à s'améliorer les performances de la roue sur le plan de la vitesse de
rotation sont diminuées
Il faut savoir que toute diminution de la vitesse d'une
machine en général diminue le rapport puissance / dimensions
L'augmentation de la masse augmente les pertes par frottement et le résultat
n'est pas aussi satisfaisant qu'on pourrait le croire , si on se place seulement
sous l'angle rendement
L'adoption d'aubes courbes oblige à augmenter la longueur de l'auget (ligne BC
pour le calcul ci dessus) et à prendre une valeur 50 % supérieure environ ,
sinon le gain en volume sera négatif
Je me suis limité au calcul d'aubes ayant par rapport aux aubes droites
l'allure du dessin ci dessous
La courbe est une parabole
La parabole est une courbe idéale , et aussi si on espère récupérer un tant
soit peu d'énergie cinétique
Il est impossible d'imposer à la courbe de passer par les points U , A , et
d'être tangente en A à AC
Cependant l'erreur commise sur b
pour la parabole est généralement faible et on peut assez facilement l'ajuster
à un écart de 1 degré max avec quelques retouches des paramètres données
C'est mieux que de rechercher une équation affinée qui peut gonfler ou
dégonfler la courbe et le résultat hydraulique ne sera pas forcément meilleur
La longueur angulaire de l'auget passe de j
à j + j
/2
On vérifie facilement que l'angle
g a pour valeur
b-j
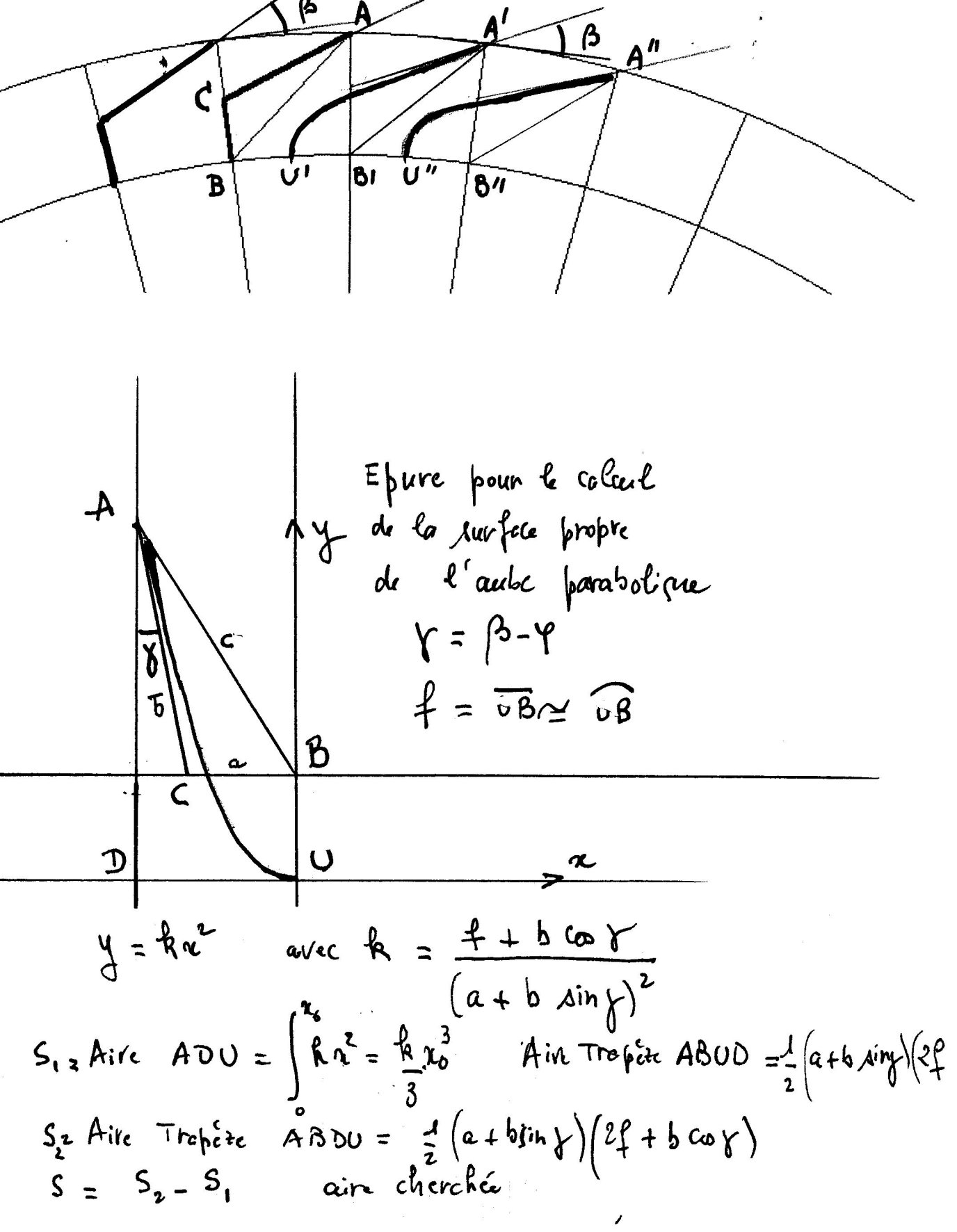
En fait le logiciel utilise une autre méthode
EXEMPLE DE CALCUL PAR LE LOGICIEL
Les résultats partiels ci dessous sont ceux d'une roue projetée avec les solutions
aubes
planes et courbes
(Chute de 8 m , tête de 0.80 , puissance 31 à 45 CV)
DONNEES
Roue de 1 m de large
Les données sont celles du débit maximum pour
chacune des options
Comme le débit a été dans chaque cas poussé au maximum des possibilités ,la
ligne de début du déversement a été avancée de 4 degrés environ (Plus pour Beta0)
Le graphique ci dessous donne le tracé fait par l'ordinateur depuis le logiciel
pour les aubes courbes avec un avancement de 50%
Rappelons que ces puissances sont celles du rendement géométrique , soit le
rendement maximum qui peut être atteint en théorie

En avançant davantage le nez , le gain de
volume devient dérisoire et des problèmes peuvent se poser au remplissage
(introduction d'air) , aussi est il sage de se limiter à 60%
Autres considérations
1 Dans le calcul il n'est pas tenu compte des pertes éventuelles par
modification des volumes d'eau "statiques" (V relative =0)
Cependant la position du centre de gravité se modifie au cours de la rotation
Ainsi si les augets ont une forme haute le passage vers l'horizontale abaisse
plus le centre de gravité que le niveau de l'eau dans l'auget
2 Pour quitter l'auget l'eau doit prendre une nouvelle vitesse relative ,
l'énergie correspondante est fournie par la hauteur résiduelle et aussi par la
force centrifuge
Ces questions , du second ordre, ont
été négligées
Dimensionnement général
Les différents organes doivent résister aux forces qui leur sont appliquées ,
aussi bien en régime normal qu'en régime perturbé
A part le diamètre de l'arbre , cette question n'a pas été traitée
Elle suppose d'ailleurs un choix sur la structure , pour laquelle diverses
options sont possibles
Réalisation d'un modèle réduit
Les formules de similitude ( données dans mon site) permettent de passer du
modèle à la machine industrielle ou l ' inverse :
Q2/Q1 = l^2
* (H2/H1)^1/2
N2/N1 =((H2/H1)^1/2) / l
P2/P1 = l^2 * (H2/H1)^3/2
Dans le cas d'une roue au dessus le diamètre est lié à la hauteur et le coefficient
de similitude s'applique aussi à cette dimension soit l
= H2/H1 ; on y gagne aussi l'avantage de conserver le même nombre
de Froude ce qui n'est pas toujours le cas pour les turbines
D'ou les formules plus simples propres à ce genre de roue :
Q2/Q1 = l^2.5
N2/N1 = l^(-0.5)
P2/P1 = l^3.5
l étant
le rapport de similitude
L'indice 1 s'appliquant au modèle réduit
Par exemple , pour une étude particulière indépendante de l'exemple vu
plus haut , on propose de construire un modèle avec l
=