Cette page affine le mode de calcul dans mon hypothèse déjà citée : une seule aube motrice à la fois.
J'attends les contradicteurs qui me donneront des preuves ...
Origine des angles
L'origine des angles pour toute position d'aube sera l'horizontale du centre de la roue à gauche de la figure
La position instantanée d'une aube est définie par l'angle a .
Dans les figures, le sens de rotation est antihoraire.
Les aubes sont séparées par un angle q en deg. tel que q = 360/n , n étant le nombre d'aubes
La vitesse amont est Vam
RECHERCHE DE LA VALEUR RELATIVE DE LA VITESSE
Soit Vr cette vitesse.
On suppose que pour toutes les positions le point d'application des vecteurs est le centre de l'aube.
Comme les premières positions ont une immersion très partielle , il en résulte une petite erreur qui est faible.
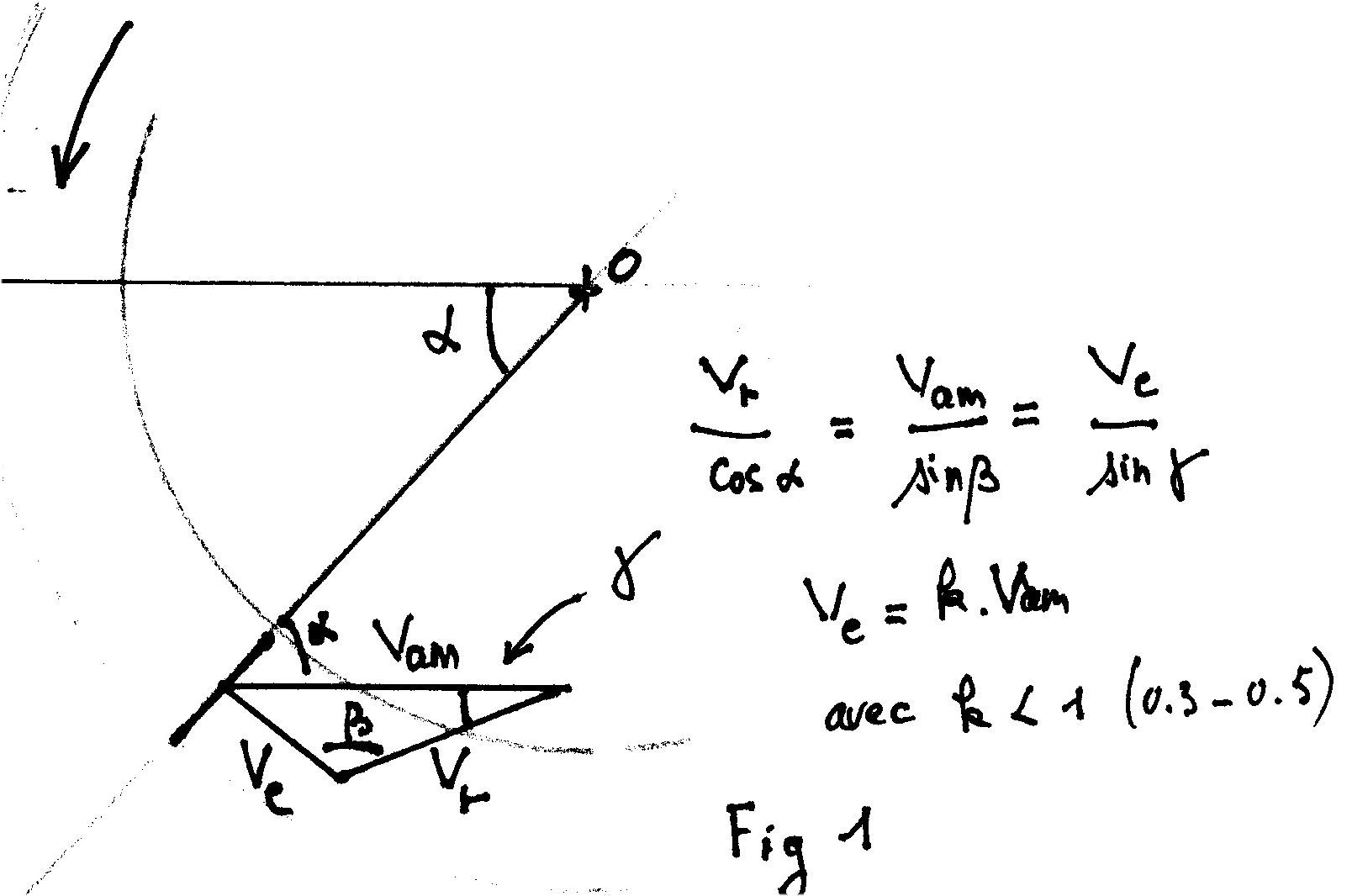
La vitesses d'entraînement Ve en ce point a une relation avec la vitesse amont Vam , de la forme Ve = k * Vam , k étant un nombre fractionnaire.
Le triangle des vitesses tel qu'il apparaît dans la figure 1 nous permet décrire les relations:
Vr/cos(a) = Vam/sin(b) = Ve/sin(g)
Ve est évidemment perpendiculaire à la plaque.
On vérifie que :
g + b - a = pi/2
et en faisant le développement de sin(b) = cos(a - g) on trouve aisément :
tg(g)= cos(a)/(1/k - sin(a))
La figure1 nous montre que la vitesse relative est bien déterminée si on fixe le coefficient de vitesse d'entraînement .
RECHERCHER DE LA SURFACE MOUILLEE
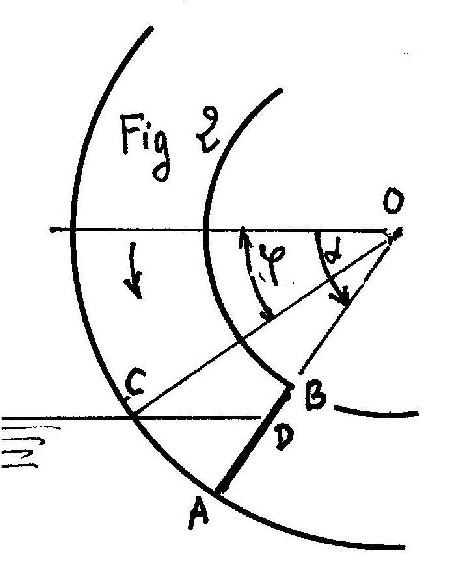
Sur la figure 2 le rayon OC est celui ou l'aube prend un premier contact avec l'eau
De plus l'aube qui vient de précéder (non représentée) se trouve à la verticale basse.
Puisque les aubes ont un pas q .on a donc j = pi/2-q
Quand elle vient en position sur OA l'aube est seulement mouillée le long de AD.
La résolution du triangle OCD ne pose aucune difficulté
On trouve
AD = D/2 *(1 - cos(j)/sin(a))
D'ou la surface mouillée en multipliant par la largeur.
La surface mouillée , donc active , augmente jusqu'à la position verticale basse.
RECHERCHE DES FORCES AGISSANTES ET DU COUPLE MOTEUR
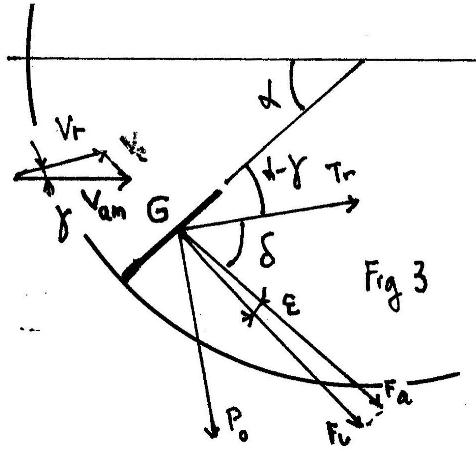La figure 3 est un peu plus complexe ; nous retrouvons les angles
a
g déjà vus.La traînée est dans la direction de la vitesse relative et la poussée bien entendu dans une direction perpendiculaire .
L'angle d est : p/2 - Atn(Tr/Po) ou encore
p/2 - Atn(Cx/Cz)
On voit que p/2 =a - g + d + e
On détermine ainsi e
La force totale Fa est projetée sur la normale à la plaque , pour donner la force utile Fu
Fu = Fa * cos (e)
