DES FORMULES ENCORE PLUS UNIVERSELLES
Aborder
cette question pourra dérouter certains lecteurs , encore que sa complexité ne
soit que moyenne
Pour comparer différentes roues sur le plan des performances (ceci est surtout
valables pour les Francis et les Kaplan) , nous avons jusqu'ici utilisé la notion de
vitesse spécifique
Une autre méthode consiste à ramener le
modèle réduit (virtuel) à une roue de 1 m de diamètre sous 1 m de chute
Cette roue sera géométriquement semblable a la roue réelle
L'intérêt est d'avoir des diagrammes immédiatement comparables sans faire de
calculs de transposition
Les indices 11
Nous définirons :
N11 = N * D / sqr(H)
t/min (01)
Q11 = Q /((D*D) * sqr(H)) l/s
(02)
P11 = P/((D*D) * H^1.5) CV
(03)
On vérifie facilement que la vitesse spécifique Ns = N11 * sqr(P11)
Les diagrammes
Si à hauteur constante on mesure pour une machine le débit , la vitesse et la
puissance recueillie et ceci en un grand nombre de points on peut porter sur un
système d'axes les valeurs de N11 en abscisse et celles de Q11 (ou P11) en
ordonnée
A chaque point de mesure correspond un rendement
Les mesures sont toujours faites sur modèle réduit car elles sont souvent
impossibles en exploitation vu la difficulté de la mesure des gros débits
Ce modèle a un diamètre qui n'est pas de 1 mètre en général mais on
fait les transpositions
Pour représenter les résultats il faudrait un système à 3 dimensions mais nous conserverons le système plan en traçant les courbes d'égal rendement
Ces courbes ressemblent à des courbes de
niveau sur une carte IGN
Aussi donne t on à ce diagramme le nom de colline des rendements
Sur le même diagramme on porte les courbes d'égaux Ns qui sont bien entendu
communes à tous les diagrammes
En fonction de ce que nous avons vu plus haut , ces courbes auraient dans un système (OX,OY) l'équation :
y = k / x^2 k étant une
constante selon la valeur du Ns
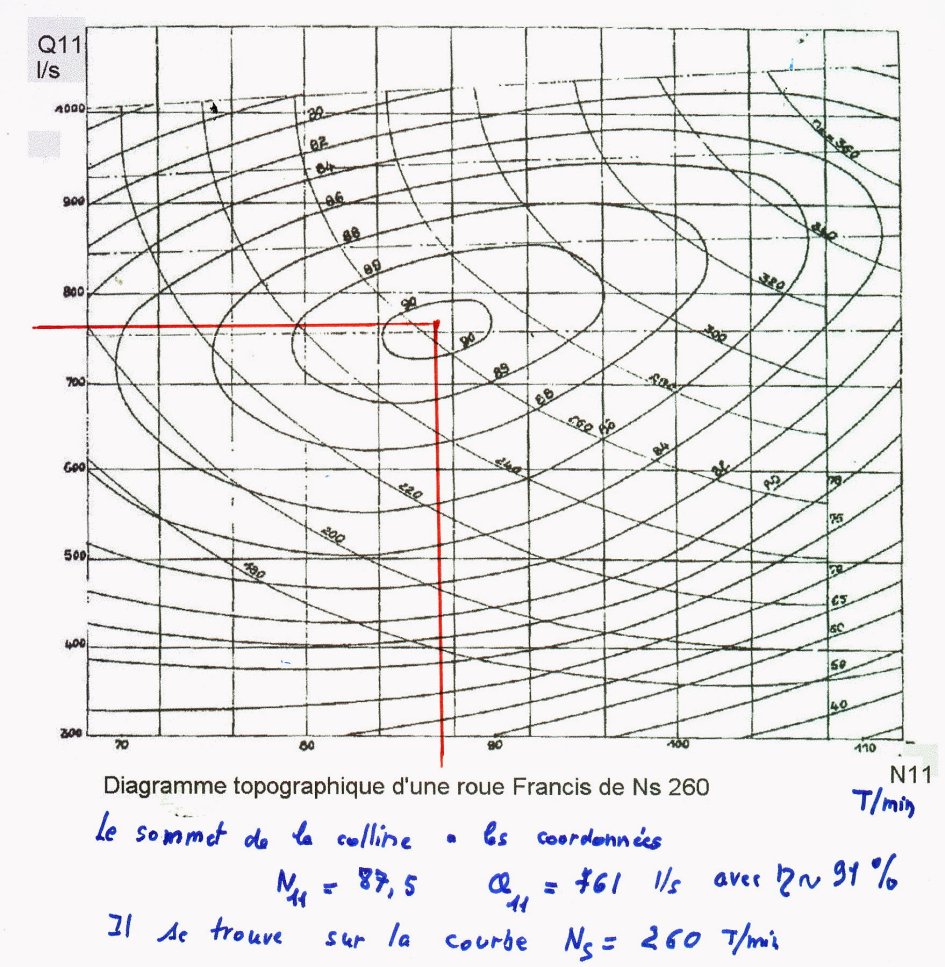
Ci dessous un diagramme d'une roue très moderne et de très bon rendement pour
une Francis

Nous ne devons pas prendre le sommet de la colline , mais un point sur
l'abscisse 87.5 qui correspond à l'ouverture max du distributeur soit Q11 =
1030 l/s
En ce point , le Ns est de 275 env. et le rendement 0.8
soient :
H = 8 m
Q = 350 l/s
La valeur de P est 8 * 350 *0.8
/ 75 = 29.86 CV
soit P = 30 CV avec neta = 0.8
avec la relation (02) nous avons
D^2 = Q /( Q11 * H^0.5) d'ou D = 0.346
N = N11 * H^0.5 /D = 715 T/min
P11=29.86 /((D*D) * H^1.5) =11.02
Le Ns pour ces valeurs est de 290 T/min
En pratique il faudra adopter la valeur synchrone de 750 T/min ce qui donne un
Ns de 300
En fait
Le diamètre de sortie de la roue est de 0.346
m. , plus grand que celui donné par
mon logiciel qui est de 0.324 mais les paramètres de cette roue sont plus
récents
Le rendement maximum reste sur le sommet de
colline à une valeur de 0.91 environ
Il est obtenu pour une ouverture de : 761/1030 =0.74 soit les 3/4
Cette valeur est parfaitement conforme aux usages
en ce point de débit est de 258 l/s et la puissance de 25 .04 CV el Ns de 278 ,
valeur un peu élevée
A ce stade nous voyons que nos calculs demandent quelques itérations pour
mieux s'adapter au diagramme et c'est le diagramme qui "domine" car il correspond à des résultats
concrets d'une roue moderne et performante
L'obligation de respecter une des vitesses synchrones gêne un peu nos calculs
Ces calculs montrent bien et comme déjà vu qu'une roue est un organe qui a une
"forte personnalité" et qu'on ne peut la manipuler comme on le ferait
d'une génératrice à courant continu par exemple , dans certaines limites
évidemment
Le diagramme permet de tracer la courbe des
rendements à vitesse constante , il suffit de considérer les interceptions de
la droite N11 =87.5 avec les courbes de rendement : on lira à chaque fois la
valeur de Q11
Les rendements réels sont un peu différents de ceux des essais
Il y des formules pour faire les retouches et c'est à partir de ces retouches
convenues à l'avance qu'une contestation peut naître entre le fabricant
et l'exploitant si la machine parait ne pas donner entière satisfaction
Cette question sort du cadre de ma
présentation
Par ailleurs la présente page a un caractère documentaire , car seuls les
professionnels peuvent en pratique utiliser ces méthodes alors que leurs essais
sont gardés dans le plus grand secret
RESUME et Raccourci
LA vitesse spécifique Ns
est la vitesse d'une roue géométriquement semblable à la roue réelle , mais
donnant une puissance effective (rendement 0.85) de 1 cv sous 1 m de chute
soit avec un débit de 88.24 litres /seconde