Rappelons que tga est la pente de la courbe du jet au point de rencontre de ce drenier  avec la roue 
Dans cette  page tous ces calculs sont faits avec un rapport des vitesses de 2 entre la vitesse de l'eau et la vitesse d'entraînement 
On suppose qu'il y a une tête d'eau
Nos calculs ont été faits avec un angle a de 7.5 °
On sait que cette valeur est trop faible et notre page sera revue
Pour le moment retenons le principe du "montage"

X est la distance entre la verticale de la sortie d'eau sous la vanne et la verticale du point de rencontre Pour éviter des calculs fastidieux nous utilisons une méthode graphique pour placer notre parabole et en même temps la tête d'eau .
Le triangle des vitesses est indéformable même si sa position varie en fonction du  choisi
C'est un triangle très plat ; avec l'approximation que nous avons faite c'est un triangle isocèle

En fait la valeur choisie pour les petits angles de ce triangle est faible et ne devrait pas utilisée pour une roue normale

Nous avons opté pour un g  de 15° correspondant au pas cumulé de 2 aubes
L' admission de l'eau est un peu retardée mais les augets supérieurs ne donnent qu'un couple très faible
 Pour le dessin de la roue nous allons utiliser une échelle de 1/10 et notre parabole à la même échelle ,celle ci tracée sur un calque
En déplacent le calque nous pouvons placer convenablement nos éléments.
 

EPURE  DES  AUBAGES

Nous poursuivons ici la réalisation de l’exemple de la roue en dessus pour donner la marche à suivre
Sur une feuille de papier Canson et avec un compas de grande ouverture traçons un fragment de cercle de rayon 22.5 cm
Nous aurons un dessin à l’échelle de 1 / 10ème
Le cercle intérieur aura un  rayon de 18.5 cm .
Traçons une verticale , et quelques rayons espacés angulairement de 7.5 ¨°  .
Chaque rayon correspond à une aube .
 Traçons pour le rayon vertical une ligne faisant un angle  b    avec la tangente au cercle , c’est a dire avec l’horizontale
Appelons A1 le point de départ de cette première ligne
cette ligne se terminera en B1 , mais pour l’instant nous ne connaissons pas la position de B1
Il faut la déterminer part tâtonnements en assurant une valeur maximale à l’angle d et la surface la plus grande possible pour définir l’auget.
Une seconde ligne partira de B1 en direction du centre des cercles et rencontre le cercle intérieur en C1
Dans ces conditions l’angle en B1 est voisin d’un angle droit ; si on prenait un angle droit le coté A1 B1 sera certainement trop long car le point B1 se trouverait à l’intérieur du prochain triangle A2 B2 C2 ce qu'il faut éviter .
Il y a donc un compromis à trouver graphiquement.
Si le nombre d’augets était différent le tracé serait différent .
En particulier si le nombre d’augets était divisé par 2 , A1 B1 pourrait pratiquement être doublé , le volume utile de l’auget serait lui aussi doublé .

On peut ainsi se rendre compte de l’importance du nombre d’augets : trop peu d’augets nuit au rendement .

Revenant à notre épure :  nous mesurons les cotés de l'auget , qui sont de 32 mm et 34 mm ; compte tenu de l'échelle et comme ces cotés forment pratiquement un angle droit , le volume (volume utile) calculé pour l'auget dont la largeur rappelons le est de 1 .20 mètres  est de 67 litres .

Cette valeur est un peu supérieure à notre valeur de départ , elle est satisfaisante
C'est ce volume qui sera occupé par l'eau tant que le 3èmè coté de l'auget n'aura pas franchi la ligne horizontale , angle que nous avons appelé q dans une autre page
Cet angle   q  mesuré sur le dessin est de 34° valeur acceptable

Il nous reste à positionner le jet d'eau
Le tableau ci dessus nous a donné une distance X de 0.68 m.
La distance X est prise à partir du point ou la ligne d'eau moyenne est considérée comme horizontale ; en effet dans la zone de contraction les filets d'eau sont courbes et s'infléchissent progressivement.

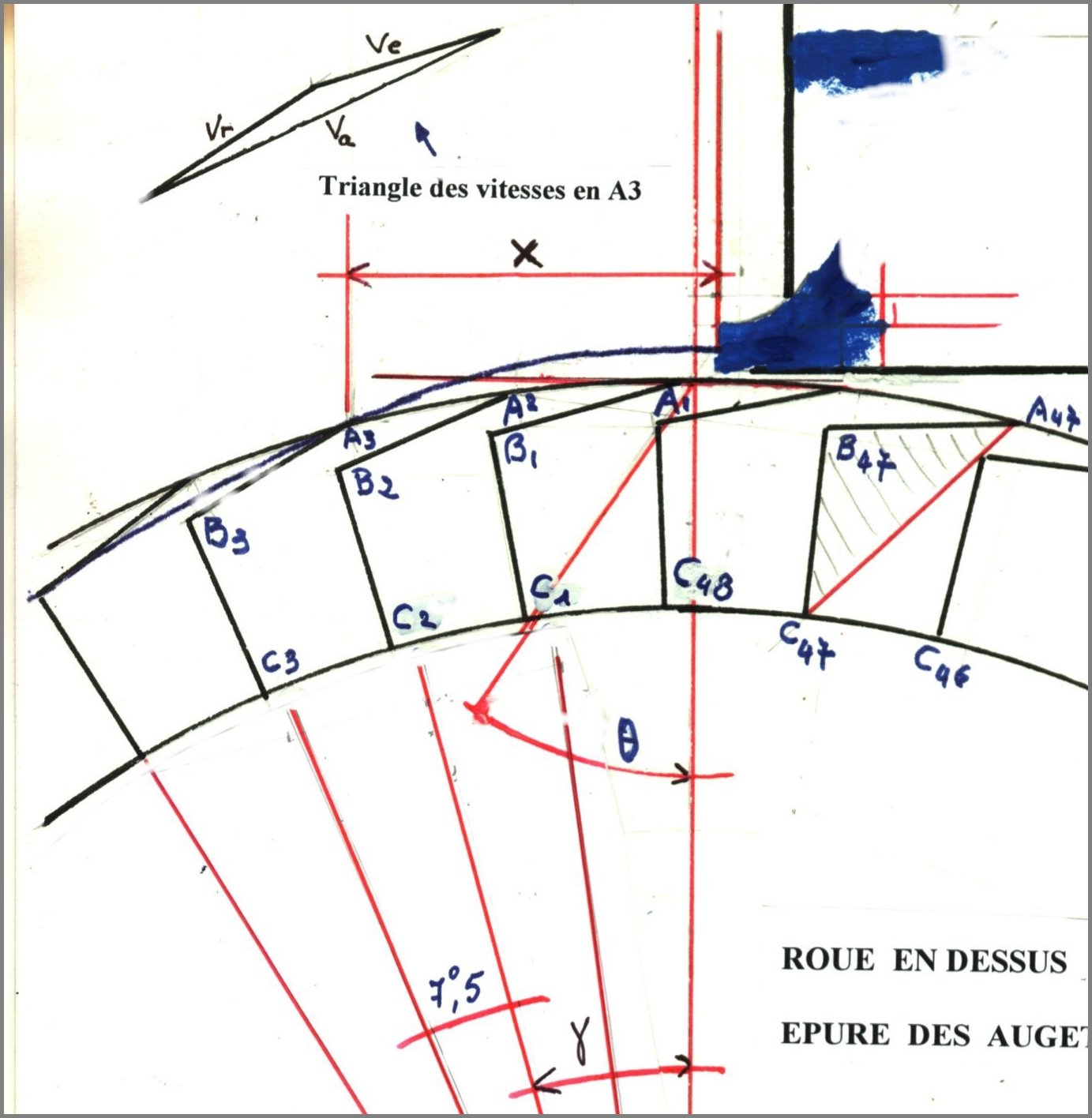
De plus on déplacera le calque de façon que la parabole coupe le cercle extérieur au point ou g = 15°
On voit que le radier du canal d'amenée est assez proche de la roue et demandera une construction soignée ; mais cette disposition minimise les pertes d'énergie comme déjà dit.

A partir du graphique et en tracent des parallèles , on peut retrouver notre triangle des vitesses conforme aux hypothèses de  départ.

Toute cette étude concerne la ligne moyenne de la lame d'eau.

En fait , la roue est arrosée par une lame dont l'épaisseur est de 8 cm comme nous l'avons vu , alors que la levée de la vanne est de 14 cm .
Dans la position du dessin , l'auget 1 est vide ; le 2 commence à se remplir , le 3 commence la fin de son remplissage .
En 1/6 seconde la lame déverse 60 litres d'eau , dont 30 litres vont dans chacun des 2 augets balayés.


Il faut noter que l'eau rencontre alternativement l'intrados et l'extrados des surfaces , et que notre calcul a été fait sur la ligne moyenne.

C'est à dire que notre calcul a eu pour but de limiter les pertes à l'admission et de tirer parti au mieux d'un type de roue dont le rôle essentiel est d'utiliser la gravité une fois que l'auget est rempli à la proportion voulue de son volume utile.
 

Retour page d'accueil