Avec l'image ci dessous , sans passer par le théorème d'Euler   , on aura une bonne approche de l'action d'un jet sur un aubage un peu évolué.
Par simplification cependant la surface concave est supposée cylindrique 
Le jet pénètre à l'horizontale avec une vitesse V et sort en faisant un angle a sort avec cette direction avec cette même vitesse 


On démontre que les composantes Rx et Ry de la force appliquée sont pour une plaque maintenue immobile :
Rx= r S * V *V * (1- cos a)
Ry= r S * V *V * sin a

r =1000 kg/m3 pour l'eau

Pour a = 90°  :  Rx = r * S * V *V = r *Q *V

Nous retrouvons la formule  du Choc d'un jet sur une surface immobile (v=0)
Cependant ici la trajectoire de l'eau est guidée.

Influence de la gravité

Si l'eau remonte comme sur la figure, elle perd de la vitesse en reprenant de la hauteur , donc , le jet s'élargit.

Cette influence sera négligeable si le terme V^2/2g est grand : cas des hautes chutes.
Pour une roue de moulin , l'influence ne sera plus négligeable

Déplacement dans le sens des X

Si notre surface recule dans le sens des x Il y aura sur la plaque une vitesse relative plus petite que V et la section de passage de l'eau est augmentée en conséquence.
Par exemple si v = V/2 la section du jet sur la plaque sera multipliée par 2
Si la plaque est régulière la vitesse relative se conserve mais sa direction est modifiée.
Avec v = V/2 la composition des vitesses à la sortie - facile à construire - donne une vitesse absolue égale à V/ sqr(2)
En élevant au carré on voit que le jet a perdu la moitié de son énergie cinétique.
Si l'angle  est de 180 ° , la vitesses relative en sortie est égale et opposée à v : la vitesse absolue est nulle.

C'est le cas idéal réalisé dans les roues Pelton.

Influence de la force centrifuge

Si le mouvement de déplacement résulte d'une rotation, l'influence ce la force centrifuge ne peut être négligée
si entrée et sortie se font sous un rayon différent.
Si on désigne par :
V la vitesse absolue
W la vitesses relative
U la vitesse d'entraînement
et avec les indices  0 pour l'entrée et 1 pour la sortie 
On démontre que pour une machine à action :
U1^2 - U0^2 = W1^2 - W0^2
Pour une machine centripète :
U0 > U1  et donc W0 > W1
La perte de vitesse relative a pour conséquence le passage de l'énergie de l'eau vers la roue.
Physiquement , ce  phénomène est par la réflexion assez difficile à saisir , mais si on prend le cas de la machine fonctionnant à l'envers , c.a.d. en pompe centrifuge , on comprend fort bien que l'eau soit éjectée puissamment par l'action de la force centrifuge et qu'alors le phénomène puisse être inverse dans le cas de la roue ou turbine.

FORMULES AVANCEES
Le théorème de Bernoulli existe aussi en mouvement relatif.
Il s'écrit
W^2 - U^2 + P / v + Z = constante

Dans le cas des machines à  action , le terme correspond à la pression atmosphérique que nous prenons pour valeur 0

De plus si entrée et sortie sont à la même hauteur pratiquement , nous prendrons aussi z=0 d'ou :
W^2 - U^2   = constante  (1)

Nous retrouverons facilement nos formules ci dessus.
De plus , dans les triangles des vitesses , si  a1 désigne  l'angle (V1,U1) et a2l'angle (V2,U2) nous avons les relations bien connues:
W1^2 = V1^2 + U1^2 - 2 U1 V1 cos(a1)
W2^2 = V2^2 + U2^2 - 2 U2 21 cos(a2)
Compte tenu de (1)
V1^2  - 2 U1 V1 cos(a1) = V2^2  - 2 U2 V2 cos(a2) ou encore
(U1 V1 cos(a1) -  U2 V2 cos(a2)) / g  = (V1^2 - V2^2) / 2g
Le premier membre désigne la hauteur manométrique récupérée par l'aube , le second l'énergie cinétique perdu par l'eau.
Si le rendement est de 100% ces 2 quantités sont bien égales  (car nous avons négligé les pertes)

TRACE D' AUBES

En plus de l'angle il faudra considérer l'angle b1 qui est celui du cercle extérieur avec l'aube à l'entrée de l'eau et l'angle b2 à la sortie.

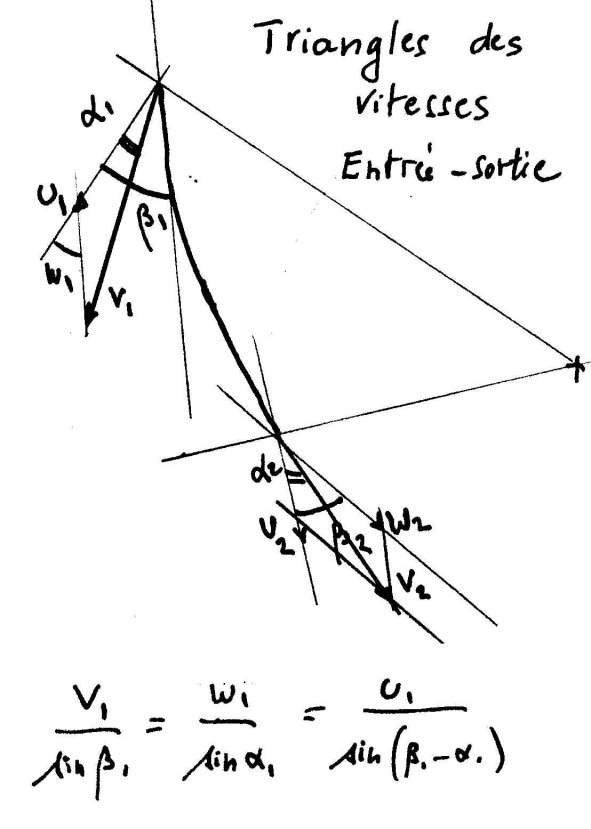
Les paramètres V1  , a1, b1, b2 définissent le comportement hydraulique de la roue.
En particulier ils permettent de calculer U1 , V2 puis W2  et a2
Quant à U2 , il se déduit de U1 par un simple rapport de diamètres.

Ces calculs se font à partir des triangles des vitesses et de leurs relations , dont un exemple a été donné et les autres formules sont faciles à retrouver.

Cependant l'aube n'est pas tracée pour autant.
Théoriquement il faudrait chercher un tracé tel que la condition soit remplie en tout point de l'aube de l'entrée à la sortie.
Pratiquement on cherchera à dessiner une courbe régulière qui remplit les conditions d'entére et de sortie.

L'expérience apprend que l'aube ne doit pas être trop courte , afin que l'échange d'énergie  " ait le temps de se faire" , ni trop longue , pour éviter des pertes de charge abusives.

Si les 3 paramètres sont mal choisis , le calcul sera impossible.
Pour ceux qui veulent faire des essais rapidement utiliser mon logiciel (à partir de la version 8.2) qui montrera ce calcul





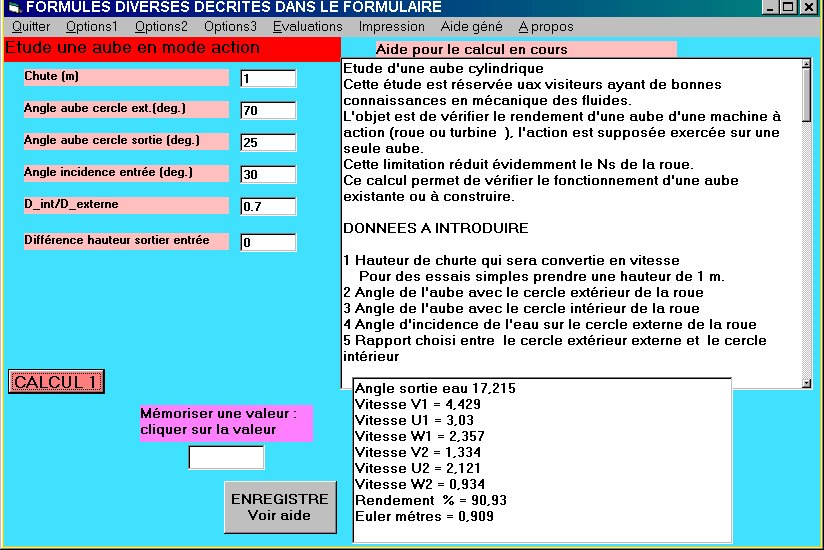
En faisant varier les paramètres, on cherchera le meilleur rendement .
Cependant il faut encore faire certaines vérifications
Les angles b1, b2 ne doivent pas être trop petits pour permettre à l'eau de s'écouler
On vérifiera la section de passage , qui doit permettre au jet entre 2 aubes de passer avec une marge de sécurité de l'ordre de 2
On peut se demander quelles sont les machines concernées par cette étude

La roue en dessous et la roue Poncelet en sont exclues car l' écoulement de l'eau ne correspond pas aux hypothèses de base .
Il est difficile par ailleurs d'adopter pour ces roues qui n'ont d'autre injecteur que le pied de vanne avec un coursier sommaire, une combinaison d'angles satisfaisants.
Ai siècle dernier , la roue Fourneyron de type centrifuge répondait à la catégorie étudiée mais la récupération de l'eau à la sortie était impossible d'ou une perte de chute
La Pelton appartient à la catégorie , mais les diamètres entrée sortie étant identiques il n'y a pas d'effet de la force centrifuge et nos équations ci dessus sont inutiles .

APPLICATIONS

CALCUL des angles pour une machine à aubes cylindriques

TURBINE FOURNEYRON
Bien que cette machine ne soit plus construite elle sera un bon exemple d'école
On donne  un bon développement à l'aube (Dext / Dint =2.17)
Avec les angles choisis la machine a un rendement manométrique de 93%
Chute (m) 10
Angle aube cercle int.(deg.) 30
Angle aube cercle sortie (deg.) 50
Angle incidence entrée (deg.) 16
D_int/D_externe 0.46
Différence hauteur sortie entrée 0
Vitesse V1 = 14,007
Vitesse U1 = 6,777
Vitesse W1 = 7,722

Angle sortie eau 89,888

Vitesse V2 = 3,707
Vitesse U2 = 3,118
Vitesse W2 = 4,839
Rendement % = 92,997
Euler mètres = 9,3

Le rendeemnt réel est bien entendu inférieur

TURBINE BANKI

Il est possible de calculer exactement les vitesses dans une roue de ce type , mais en faisant 2 passages du calcul , l'un pour la phase centripète , l'autre pour la phase centrifuge du crossflow.
Bien entendu dans la seconde phase on inversera les angles et le rapport D2/D1 qui dans notre exemple passera de 0.66  à 1.5
L angle d'injection en phase 2  sera l'angle de sortie de la phase1

Chute (m) 10

Phase 1

Angle aube cercle ext.(deg.) 30
Angle aube cercle sortie (deg.) 90
Angle incidence entrée (deg.) 16
D_int/D_externe 0.66

Vitesse V1 = 14,007
Vitesse U1 = 6,777
Vitesse W1 = 7,722
Vitesse V2 = 7,329
Vitesse U2 = 4,473
Vitesse W2 = 5,805
Angle sortie eau 52,386
Rendement partiel1 % = 72,625
Euler mètres = 7,262

Phase 2

Chute (m) 2.8 = hauteur correspondant à V2
Angle aube cercle int.(deg.) 90
Angle aube cercle sortie (deg.) 30
Angle incidence entrée (deg.) 52 = angle sortie ci dessus
D_externe/D_int  1.5

Angle sortie finale eau 88,099
Vitesse V1 = 7,329
Vitesse U1 = 4,563
Vitesse W1 = 5,841
Vitesse V2 = 3,88
Vitesse U2 = 6,845
Vitesse W2 = 7,755
Rendement partiel2 % = 72,601
Euler mètres = 2,033

Euler total 9,295
Rendement global théorique % 92.95

En fait nous avons pris des coefficients de 1 pour les injections , ce qui revient à dire que l'énergie est transformée en énergie cinétique avec un rendement 1 
En fait ce rendement est de 0.98 pour un injecteur bien tracé
Le rendement théorique tournerait ainsi autour de 90 - 91 %

Pour l'entrée dans le second passage , certains auteurs prennent encore un coefficient réducteur de 098 entre la vitesse sortante et la vitesse entrante
Cette hypothèse ne me parait nullement fondée
Mais ce qui est plus grave est la grande perturbation à l'intérieur de la roue par suite des interférences entre les jets provenant des aubes successives
Pour plus de renseignements à ce sujet me demander l'envoi du fichier Banki.pdf 


Pour un calcul total de la roue on choisira vitesse de rotation et diamètre de façon que 
la vitesse circonférentielle de la roue soit compatible avec la vitesse périphérique (ici 6.8 m/s)
On peut faire l'épure mais nous savons déjà que nous pouvons prendre des arcs de cercle.
Vérifier le débit passant entre 2 aubes comme dit ci dessus.
En déduire la largeur de la roue pour le débit à turbiner.