APPROCHE DE LA TURBINE BANKI

Imaginée par l'ingénieur australien  A. G. M. Michell, qui obtint un brevet en 1903 .
Ensuite la turbine fut indépendamment de cette invention réinventée en Allemagne par le professeur hongrois Donat Banki en 1917 
Un modèle réduit opérationnel se trouve à Munich au Deutsche Muséum ; la roue a 200 mm de diamètre et comporte 40 pales.
Cette roue est aussi connue sous le nom de Crossflow ou encore Oessberger : voir ci après

Cette roue semble avoir été dédaignée par les grands constructeurs français , sans doute à cause de son rendement qui est en tous cas inférieur à celui des performantes Francis et autres types rapidement décrits dans d'autres pages de ce site.
Mais cette roue a un avantage : sa construction est simple , son calcul est facile et la construction peut être envisagée au stade artisanal et même pour les petites puissances , par un bon bricoleur !
Dans cette roue en effet il n'y a pas de surfaces gauches , les aubes sont des portions de surface cylindrique circulaire.
On peut donc les découper dans du tube , en acier , laiton, ou même plastique.

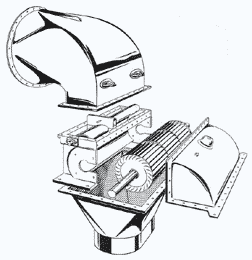
Il faut cependant faire une distinction entre la turbine Banki et le type Oessberger qui en est dérivé est en fait celui qui est représenté sur la figure ci dessus et sur la suivante
Dans cette machine l'admission se fait sur plusieurs aubes à la fois comme le montre la figure


 ci dessus qui donne un  aperçu de la coupe de cette machine et l'image en couleurs illustre mieux le trajet de l'eau qui correspond à une admission sur un assez grand nombre d'aubes

La Banki initiale a par contre a une admission sur une seule largeur entre 2  aubes

La turbine Banki ou Crosflow convient pour des débits de 20 à 1000 l/s et des chutes de 1 à 200 mètres. Elle est aussi appelée turbine à flux traversant car sa particularité est que l'eau traverse deux fois la roue.

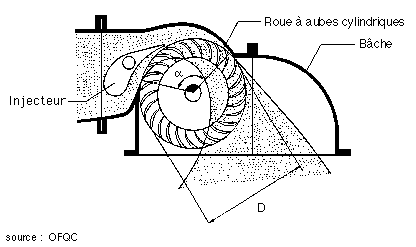
De construction simple, elle est constituée de trois parties principales :

- un injecteur de section rectangulaire et dont le débit est réglé à l'aide d'une aube profilée rotative, similaire à une vanne papillon. Afin d'assurer un arrêt de la turbine sans énergie d'appoint, la fermeture est souvent réalisée à l'aide d'un contrepoids et l'ouverture par un vérin hydraulique,
- une roue en forme de tambours, dotée d'aubes cylindriques profilées,
- un bâti enveloppant la roue sur lequel sont fixés les paliers de la turbine.

Avant d'aller plus loin il faut expliquer le principe de cette roue qui a quelque parenté avec  celui de la Pelton.

RETOUR SUR LA PELTON

Quand un jet d'eau attaque une plaque il n'y a pas de perte d'énergie si la plaque est tangente au jet (absence de choc comme dit à plusieurs reprises)

Si la plaque s'incurve avec un tracé régulier il en sera de même ; l'eau quittera la plaque sans avoir perdu de sa vitesse donc de sa puissance .
Les choses changent si la plaque est en mouvement , c.a.d. si elle recule sous l'effet du jet .Nous avons déjà vu cette question.
Supposons que la plaque soit une portion de demi cylindre et recule à une vitesse moitié de celle du jet.
Les triangles des vitesses se réduisent à des segments de droite ;le tableau simple ci dessous donne les valeurs des vitesses

On a toujours la relation connue Va = Ve + Vr
On constate immédiatement qu'à la sortie l'eau a perdu tout son énergie et comme il n ' y a pas eu de pertes le long de son parcours , l'énergie a été récupérée par la roue qui porte cette surface.
A la sortie l'eau se "contente" de tomber par gravité !
Ce mode de calcul par les vitesses et les énergies est le plus simple qui soit .
Telle est du moins la théorie simplifiée , proche de la réalité car dans une bonne Pelton , ou la géométrie des augets est évidemment très améliorée par rapport à notre demi cylindre , les rendements sont supérieurs à 90 %

LA BANKI
Comme dans la Pelton nous sommes en présence d'une turbine de type atmosphérique : à partir du moment ou l'eau entre dans la roue la pression est nulle , nous sommes en présence d'un jet qui va être dévié par les aubes. et sortir à l'air libre.
Si on n'a pas compris cette particularité le fonctionnement de la Banki demeure mystérieux .
En effet si on était sous pression par exemple dans les aubages d'entrée il faudrait appliquer partout la relation de continuité du débit et les triangles des vitesses seraient impossibles à  déterminer.
Ensuite c'est la vitesse relative qui entre en jeu ; les auteurs admettent que l'eau remplit l'espace entre aubes à sa première sortie.
On a peut être déjà compris que l'eau va traverser 2 fois les aubages , après avoir effectué un trajet à l'intérieur de la roue.

Nous savons déjà que l'idéal serait d'avoir une vitesse nulle à la sortie , du moins , aussi faible que possible.
C'est cette question que nous allons étudier et à partir de maintenant il y a quelques calculs (qui seront encore plus développés par la suite) .

Première analyse.
On veut d'abord chercher à comprendre le fonctionnement de cette roue.
Nous nous plaçons dans le cas de l('injection sur une seule portion de roue comprise entre 2 aubes

Pour cela nous étudions la trajectoire de l'eau depuis son arrivée en A , sa sortie provisoire en B , sa ré injection en C et sa sortie définitive en D .
Le diagramme a été établi à l'échelle d'une roue véritable.
Sur mon dessin original les dimensions sont à l'échelle 1/20 , les vitesses sont à l'échelle de 1 cm pour 1m/sec.
Les aubes sont des arcs de cercle dont le rayon est voisin de la différence entre les rayons des  2 grands cercles

La vitesse absolue Va forme avec le cercle externe un angle a que Banki a déterminé comme devant être égal à 16 °
De plus le cercle externe forme avec l'aube à son intersection un angle de 30° environ ; c'est aussi l'angle de la vitesse relative Wa avec la vitesse périphérique Ua

La vitesse Va est de 10m/sec , elle frappe la roue sous cet angle a

Avec le cercle interne l'angle est de 90° , condition nécessaire pour une sortie radiale de la vitesse relative.

L'eau sort donc avec une vitesse absolue Vb que l'on retrouve en Vc inchangée
Cette vitesse est déjà nettement inférieure à Va
Remarquons que les triangles des vitesses en B et en C sont de dimensions identiques.
Finalement l'eau sort en D Vd avec une vitesse environ 4 fois moins grande qu'à l'entrée , mesurée à l'échelle du dessin.

L'énergie définitivement perdue avec cette valeur est donc seulement 1/16 de l'énergie initiale ,
soit 6 % et  un rendement théorique maximum de 94 %.
Il est certain que par un affinement du graphique on peut encore diminuer la valeur de 4.
Certains fabricants affirment avoir une perte à la sortie de 1% seulement.

La trajectoire de l'eau  en pointillé est la trajectoire absolue par rapport à un référentiel lié au sol ; la trajectoire dans la roue se fait le long de l'aube ou parallèlement à elle selon l'épaisseur de la lame d'eau , et pour qu'il y ait échange d'énergie

Compléments

Pratiquement comme Wa est numériquement assez peu différent de Ua (en fait Wa/Ua est d'environ 1.15 selon des calculs plus poussés ) on peut reporter la longueur de l'arc  ou sa valeur corrigée sur le grand cercle pour obtenir la position d'aube qui donne le point B "exact !"

Le rendement manométrique à partir des formules d'Euler
L'eau traverse 2 fois la roue 
A chaque passage elle donne une partie de son énergie cinétique à l'aube 

Il est possible de calculer exactement les vitesses dans une roue de ce type , mais en faisant 2 passages du calcul , l'un pour la phase centripète , l'autre pour la phase centrifuge du crossflow.
Bien entendu dans la seconde phase on inversera les angles et le rapport D2/D1 qui dans notre exemple passera de 0.66  à 1.5
L angle d'injection en phase 2  sera l'angle de sortie de la phase1

Les calculs sont faits avec mon logiciel général (Option action de l'eau sur une aube) en considérant une chute de 10 m
Le triangle des vitesses à l'entrée est redessiné ci contre , ceux des autres points s'en déduisent facilement - voir les figures plus haut

Ce dessin rappelle toutes les formules pour passer des vitesses V à U et W en fonction de l'angle d'incidence et du coefficient m de vitesses périphérique
On a pris m = 0.48

La vitesse W2 peut s'obtenir facilement par l'équation de continuité du débit  soit , en désignant par t1 l'arc intercepté par le jet externe et t2 celui du cercle interne:

t1 * sin(b1) * W1 = t2 * W2
et comme t1/t2 = 1.5 et sin(b1)=0.5 avec b1 = 30 °
W2/W1 = 0.75

Les calculs en italiques sont ceux de l'ordinateur

Ils montent que le premier passage est énergiquement bien plus efficace que le second , a priori on pouvait s'en douter

Chute (mètres) 10

Angle incidence entrée (deg.) 16
Angle aube cercle ext.(deg.) 30
Angle aube cercle sortie (deg.) 90
 D_int/D_externe 0.66

Angle sortie eau 52,386
Vitesse V1 = 14,007
Vitesse U1 = 6,777
Vitesse W1 = 7,722
Vitesse V2 = 7,329
Vitesse U2 = 4,473
Vitesse W2 = 5,805
Rendement partiel1 % = 72,625
Euler mètres = 7,262

Phase 2

Chute (m) 2.8 = hauteur correspondant à V2
Angle aube cercle int.(deg.) 90
Angle aube cercle sortie (deg.) 30
Angle incidence entrée (deg.) 52 = angle sortie ci dessus
D_externe/D_int  1.5

Angle sortie finale eau 88,099
Vitesse V1 = 7,329
Vitesse U1 = 4,563
Vitesse W1 = 5,841
Vitesse V2 = 3,88
Vitesse U2 = 6,845
Vitesse W2 = 7,755
Rendement partiel2 % = 72,601
Euler mètres = 2,033

Euler total 9,295
Rendement global théorique % 92.95

Cette valeur est confirmée par la considération des carrés des vitesses entrée sortie

En fait nous avons pris des coefficients de 1 pour les injections , ce qui revient à dire que l'énergie est transformée en énergie cinétique avec un rendement 1 
En fait ce rendement est de 0.98 pour un injecteur bien tracé
Le rendement théorique tournerait ainsi autour de 90 - 91 %


Puissance
On se reportera à la formule générale et bien entendu on tiendra compte du rendement .
Pour un avant projet on peut prendre une valeur de 0.7 pour le rendement.
Cette valeur sera confirmée ou infirmée par les essais.

Vitesse spécifique 
Si on fait le calcul du Ns on trouve des valeurs de l'ordre de 40 à 80
Cette valeur n'est pas très élevée ,  les roues ne tourneront pas très vite par rapport à des roues beaucoup plus rapides telles que les hélices.
(En compensation , leur exploitation avec des eaux chargées de débris est bien plus facile)

CALCUL DES DIMENSIONS

LA TURBINE OSSBERGER ( plus de détails , document fabricant)

Retour page d'accueil