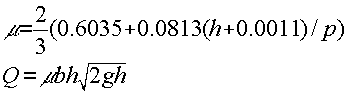Formules courantes
Formules utilisées dans nos calculs et quelques
autres
Dans toutes les formules le signe * est le signe de multiplication
Certaines formules ont été écrite en caractères mathématiques , d'autres
non , cette présentation pourra s'améliorer par la suite .
Le séparateur décimal est le point et non la
virgule
La dite remarque s'applique à la totalité du
site
Vous pouvez disposer d'un logiciel qui calculera pour vous
toutes ces formules
Vitesse/Hauteur
Une formule très courante en hydraulique est
la relation vitesse hauteur
elle donne la vitesse de l'eau qui sort d'un orifice ou la pression amont
évaluée en hauteur d'eau est H

H est en mètres , V en mètres/sec
et g est l'accélération de la pesanteur
Equations aux dimensions (facultatif !)
Les curieux pourront chercher à savoir ce
qui se cache derrière les formules
Les unités primaires du système légal sont le mètre , la masse et la seconde
Dans la formule ci dessus g est une
accélération , homogène à une longueur divisée par le carré d'un temps
g est homogène à L T-2
2gh sera donc homogène à L2 T-2
V sera homogène à L T-1 qui est la racine du précédent
La vérification de l'homogénéité permettra d'éviter des erreurs de calcul
grossières si on s'aventure seul dans les calculs ....
Vannes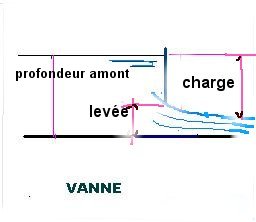
Débit d'une vanne simple
Comme formule bien approchée nous prendrons
S étant la section de passage

h=charge=différence de hauteur entre le niveau haut et le dessus de la lame
d'eau stabilisée sortant de la vanne , en mètres
La section est en m2
Q est en m3/seconde
K varie de 3.2 à 3.0 selon les dimensions et l'ouverture de la vanne
Attention : il y a lieu de bien choisir la valeur de h
qui correspond à la surface libre de la veine
Exemple vanne de largeur 1.2 mètres
La hauteur d'eau en amont est 0.60
Déversoir
Très utilisé pour la mesure des débits partout ou il est possible d'en
l'installer un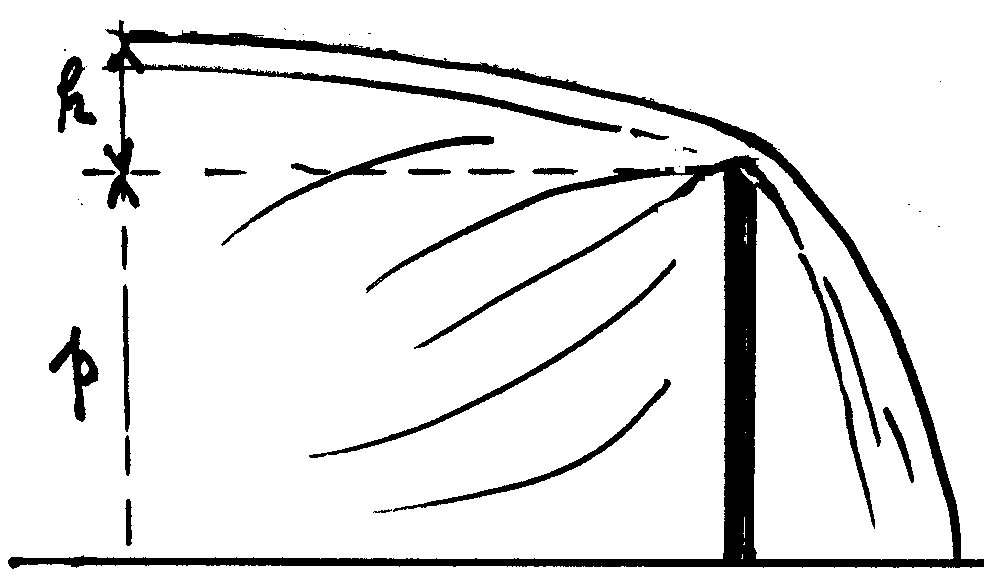
La formule la plus simple
Q = 0.41 * B * h * racine(2gh)
h est la charge en m. (voir dessin) elle doit être mesurée depuis loin
à l'amont
B est la largeur en m.
Q est en m3/s
Cette formule ne fait pas intervenir la profondeur p , aussi est elle
approximative
Un calcul plus précis utilise le paramètre p
Mon logiciel utilise la célèbre formule de
Rehbock :
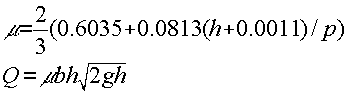
Détails avancés
Puissance d'une
chute
La puissance théorique valable pour toute
installation est donnée par la formule
P = 0.01333 * Q * H en CV
ou pour employer des unités proches des légales :
P = 9.81 * Q * H en watts
Q est le débit de la chute en litres/seconde
Si Q est en m3/sec alors
P = 13.33 * Q * H en CV
ou pour employer des unités proches
des légales :
P = 9.81 * Q * H en kilowatts
C'est la plus classique que l'on traduit souvent en tenant compte d'un certain rendement
global
Pu = 7 * Q * H (Pu puissance utile en kW
Q m3/s H mètres)
Ex H = 10 m Q =3 m3/s Pu = 210 kW aux bornes de sortie de l'alternateur
Pour les puristes la formule rigoureuse en légales S.I. est :
P= v
* g * Q * H en watts avec g = 9.81 m/s/s , v
= 1000 kg/m3 , Q en m3/s , H en m
H est la hauteur de chute nette en mètres
Pour avoir la puissance réelle il faut multiplier par le rendement ,
coefficient < 1
Calculs très rapides avec mon logiciel !
Choc
d'un jet sur une surface fixe ou mobile
Quand un jet d'eau animé d'une vitesse V rencontre une surface à angle droit il exerce sur
cette
surface une force
F = v
*Q * (V-v)
F force en Newtons
Q débit en m3 /seconde
V et v en m/s
v
étant
la masse spécifique de l'eau en kg/m3 soit 1000
v vitesse de recul de la plaque dans la direction du jet
Pour ceux qui s'intéressent aux équations aux dimensions
F est homogène à M L-3 L3 T-1 L
T-1 soit M L T-2 (produit masse accélération)
Cette formule peut aussi se déduire de l'équation F=M * (V-v)
, équation de la percussion obtenue par la prise en compte des quantités
de mouvement .. Dans ce cas M est la masse par unité de temps.
Exemple
V=60 m/s
Q =0.6 m3/s
Si v=0 (plaque immobile) on trouve F=36000 N
Cet exemple correspond à une chute d'eau avec H=183.5 m et Q =0.6 m3/s
La puissance théorique de cette chute (avec rendement unité) est de 1080000
watts (1080 kW)
C'est cette même valeur que l'on retrouve si on considère l'énergie
cinétique du jet , soit 1/2 M * V * V
Cas de la puissance
Pour une plaque plane :
Si la surface est immobile celle ci ne récupère aucune énergie , mais
l'eau conserve une énergie propre en quittant la plaque
Dans le cas de la plaque immobile , une
question qui se pose est de savoir quelle est la perte d'énergie due au choc.
Je n'ai pas de trouvé de réponse à ce problème
complexe
Si v n'est pas nul la puissance récupérée est F * v
Si enfin v= V/2 la puissance passe par un maximum
soit donc P=
r
*Q * V * V / 4
La formule complète est P=
r
*Q * v * (V -v )
P est nulle pour v=0 et v=V
Elle est max comme déja dit pour v = V/2 car alors la dérivée
dP/dv est nulle
.
Il s'agit de la puissance récupérable par une
plaque plane .
En reprenant notre calcul avec v=V/2 on trouve une puissance de 540000
watts , moitié de la puissance totale .
Cette récupération ( en théorie, mais vérifiable par des expériences
correctes ) en fonction de la forme est donc :
La moitié de l'énergie
du jet pour une plaque plane rencontrant le jet perpendiculairement
La totalité (en théorie ) pour
une surface courbe renvoyant l'eau en sens inverse de la
direction du jet (cas d'une hémisphère , ou des turbines
Pelton ; et aussi Banki )
Dans ce cas notre valeur de P est à multiplier par 2
Remarque : On verrait sans peine que P est homogène à
M L2 T-3
Jet sans choc
Cette question est traitée avec les machines
à action
Energie et Puissance
Certains visiteurs ne distinguent pas bien ces 2 notions
Une masse de 1 Kg située à 1000 m d'altitude a par rapport au niveau de la
mer une énergie (potentielle) de
10000 joules
Si elle tombe au niveau zéro elle libère son énergie ; la chute non contrôlée
conduit à une dégradation : l'énergie se perd en chaleur.
Mais on peut imaginer un système mécanique pour récupérer l'énergie , par
exemple la chute sur une plaque (robuste ! ) fera remonter de 1 mètre une masse
de 1000 Kg.
Si toutes les secondes une nouvelle masse suit la précédente et active une
machine bien étudiée celle ci recevra une énergie de 10000 joules par seconde
ce qui correspond à une puissance de 10000 watts
1 watt = 1 joule par seconde
On suppose dans tous les cas que le rendement est parfait ce qui est loin de
la vérité car la résistance de l'air fausse le calcul.
Revenons à notre énergie de 10000 joules
Elle équivaut à 10000/4.18 =2392 calories (petites) soit 2.392 Kcalories
1 Kg de charbon de bonne qualité a une énergie interne de 8000 Kcalories
Si on le brûle dans une centrale thermique et si on transforme la
chaleur en énergie mécanique avec un rendement de 30% on récupère 2400
Kcalories soit l'équivalent de 3 Kwh environ.
En fait il faut déjà une centrale performante pour arriver à ce résultat :
chaudière à haute pression , condenseur.
L'énergie nucléaire est convertie en énergie électrique avec un
rendement de cet ordre.
Les locomotives à vapeur avaient un rendement de 5% à peine !
Théorème
de Bernoulli
Ce théorème essentiel découvert par Bernoulli (1700 - 1782) nous montre que l'énergie
spécifique par unité de poids d'un fluide non visqueux (pour nous
, de l'eau )
dans un écoulement sans pertes de charges est constante
P + H + (V * V / 2 / g) = constante
P : pression du fluide évaluée en mètres d'eau
Si la pression est en Pascals il faut remplacer P par P /
v
, v étant le poids spécifique en Newton
par M3.soit 10000 pour l'eau
H hauteur du point d'observation considéré par rapport à un niveau de
référence arbitraire mais fixe .
V vitesse du fluide en mètres par seconde
Equation d '
Euler
Bien que cette équation soit un peu abstraite
je la donne pour mes lecteurs habitués à ce genre de raisonnement
Elle n'est pas indispensable pour comprendre les machines
Considérons une masse de fluide circulant entre 2 aubes d'une turbine , donc
entre l'entrée et la sortie
Nous avons pu voir à propos de certaines machines , la roue au dessus par exemple,
comment se présentaient les triangles de vitesse .
Nous allons considérer les variables d'entrée et de sortie
L'indice 0 sera pour l'entrée et l'indice 1 pour la sortie
V désigne la vitesse absolue de l'eau
U sa vitesse d'entraînement (de par la rotation de la roue)
W sa vitesse relative qui d'ailleurs n'intervient pas dans la formule
Un la composante de la vitesse absolue selon la vitesse d'entraînement (en
fait c'est la vitesse giratoire de l'eau )
La formule est
Heff = (U0 * V0N - U1 * V1n) /
g
C'est une des équations d' Euler
Heff est la hauteur de chute récupérée par la roue en mètres
Les autres variables sont en m/s
Le nombre d'aubes est supposé infini et le liquide , parfait , c.a.d.
sans viscosité.
Pour que la relation soit applicable sans
pertes de l'entrée à la sortie , il faut un écoulement sans décollements
tout le long des surfaces .
Cette condition demande qu'en chaque point de l'aube ; la vitesse relative
soit tangente à la surface de l'aube
, condition difficile à remplir d'ou la difficulté
d'un bon tracé des aubes .
Par ailleurs la formule exacte suppose le nombre d'aubes infini
Cette relation n'est pas applicable aux
roues verticales qui n'ont pas à proprement parler de bord d'entrée et de
bord de sortie , mais elle s'applique bien aux roues horizontales;
Pertes de charge
Tout fluide qui circule à l'air libre ou en
canalisation subit une dégradation d'énergie appelée perte de charge.
Cette perte existe dans les lignes droites (dues à la rugosité et au
frottement) , elle est très accentuée par les changements de direction , les
variations de section.....
Il est d'usage d'affecter à ces pertes , locales notamment , un coefficient par
rapport à la quantité connue : V * V *2 *g
Ce coefficient est souvent désigné par la lettre
x
Ces coefficients ont été étudiés le plus souvent expérimentalement. et de
nombreux facteurs interviennent notamment les diamètres et l'état des parois.
Pour le moment je dois renvoyer le lecteur à des formulaires , car la nature
des parois le diamètre et la nature de "l'obstacle"
compliquent le problème.

A titre d'exemple , je montre dans cette image les coefficients à
appliquer au départ ou à l'arrivée d'une conduite dans de larges
réservoirs
Ces coefficients sont à multiplier par la quantité V*V/(2*g) ce qui suppose
que la vitesse a pu être calculée
Le produit obtenu est évidemment en mètres d'eau
Pour des coudes à 90° non brusques la valeur de
x est
de l'ordre de 0.3 mais attention cette valeur ne peut être utilisée dans un
calcul sérieux , ici elle est indicative
Pertes de charge dans les canaux
formule de Manning
jp = 1000 * V * V * NdeMani * NdeMani * (Rh ^ (-4 / 3))
jp = perte de charge mm/m
V vitesse de l'eau m/s
Ndemani coeficient de manning
voir la table
attention ne pas confondre avec le coeff de Strickler qui est son inverse
Rh rayon hydraulique = surface mouillée / périmètre mouillé
Formule de Bazin
soit A =1000 * (1-g
/ Rh^0.5) ^2
et
B= (87)^2 * Rh
jp = A/B
g
varie de 0.06 (lisse) à 1.75 (très rugueux)
Modèles
Ce paragraphe concerne uniquement les
utilisateurs de mon logiciel
3 Modèles hydrauliques d'écoulement dans
une conduite en charge ont été crées avec un maximum (?) d'explications
L' écoulement dans une conduite en charge étant un peu plus difficile à
saisir que celui d'un canal à l'air libre
Puissance
mécanique d'un jet
La puissance mécanique d'un jet d'eau est l'énergie par seconde contenue dans ce jet
Elle dépend de la vitesse et du débit
Pm =0.5 * Q * r
*V *V = 0.5 * S *V*V*V * r
r
étant
la masse spécifique de l'eau en kg/m3 soit 1000
Q est le débit en m3 par seconde
S est la section du jet en m2
V est en m/sec Pm en watts
Obstacle
dans un fluide en mouvement
Tout obstacle dans un écoulement
reçoit une réaction de la part du fluide.
La force exercée dans le sens du courant porte le nom de traînée.
La force exercée perpendiculairement
au sens du courant porte le nom de portance
On utilise ces propriétés en aérodynamique ; une aile d'avion se comporte de
cette façon en mouvement relatif ; on cherche alors des profils de grande
finesse : grande portance , faible traînée.
Une plaque totalement en travers du courant agit de façon strictement opposée
: la portance est nulle , la traînée considérable.
Ainsi une plaque assez mince reçoit dans l'eau une poussée (traînée) évaluée
à :
F =600 * S * V *V
F en Newtons
S en m2
V en m/s
Si la plaque recule à une vitesse v , la formule devient
F =600 * S * (V-v)^2
Elle reçoit une énergie W=F*v exprimée en watts
Il faut noter que les interactions
sont identiques , que le fluide soit en mouvement et l ' obstacle
immobile , ou l'inverse
Ecoulement laminaire
Type d'écoulement peu rapide dans
lequel les pertes de charge le long des parois (canaux , conduites) sont
proportionnelles à la vitesse de l'eau
Ce type d'écoulement ne se rencontre guère dans les machines hydrauliques ,
sauf éventuellement dans la roue Sagebien
Ecoulement turbulent
Type d'écoulement rapide dans lequel les pertes de charge le long des parois
(canaux , conduites) sont proportionnelles au carré de la vitesse de l'eau
La différence entre les 2 formes est fonction d'un nombre appelé nombre
de Reynolds ou interviennent vitesse ,
dimensions, viscosité
Le nombre de Reynolds est défini par
R = U * D / n
U vitesse de l'eau en m/s
D diamètre de la conduite en m
Dans le cas d'un écoulement à l'air libre (canal) on prend D = 4 fois le rayon
hydraulique
n coefficient
de viscosité cinématique en métres carrés par seconde
Pour l'eau à 15° n
= 1.15 *10^*6 =
0.00000115 m2/s
Exemple D=0.1 m U= 0.2 m/s
R = 1000000 * 0.1 * 0.2 / 1.15 = 20000/1.15 = 17400 env.
Cette valeur caractérise un écoulement très turbulent
On démontre que la valeur limite est 2500 pour R ce qui suppose que le produit
U*D soit < à 0.0028
Il en résulte que les écoulements laminaires seront dans notre
étude rarissimes
Ecoulement
torrentiel
Un écoulement de type torrentiel est celui que l'on trouve au pied d'une
vanne ouverte suivie d'une pente , par exemple.
Ce type d'écoulement , à grande vitesse , ne peut se maintenir que si la pente
du radier a une certaine valeur minimale, dite pente critique (torrents de
montagne).
Dans ce type d'écoulement , la valeur du terme v * v / 2g a une valeur
importante .
Si la pente devient insuffisante , il y a ressaut ..
Après le ressaut ; il y a eu une perte considérable d'énergie.
Le contraire de l'écoulement torrentiel est l'écoulement fluvial
On perle aussi de subcritique (fluvial) et supercritique (torrentiel)
Ne pa confondre avec les formes laminaires et turbulentes
Puissance et couple
Quand l'énergie mécanique est "rotative" et non plus
"linéaire" le produit Force * vitesse est remplacé généralement
par Couple * Vitesse angulaire
P = C * w Ne
pas confondre v
et w
P en watts
C en mN
w en
radians par seconde : (w
= 2 *
p
* N / 60)
, N en T/min
Exemple "linéaire rotatif"
Une voiture dont le moteur développe effectivement 50 CV et dont la vitesse
est 36 m/s (130 km/h) doit vaincre une résistance de 1022 Newtons
(surtout résistance de l'air , en gros équivalente à celle d'une plaque plane
de 1/2 m2)
Si le moteur tourne à 5000 T/min il doit produire un couple de 70.28 mN
(avec rendement 1 pour la transmission)
Autre exemple une assez grosse visseuse qui
doit vaincre un couple de 10 mN en tournant à 1 t/sec
consomme une puissance mécanique de 62.8 watts
10mN : une masse de 1 kg qu'il faut soulever au bout d' un bras de levier de 1 m
Vérifiez ces formules si
voulez vous familiariser avec ces notions
Diamètre d'un
arbre

K=96 à 120 selon la sécurité désirée
P en CV
N en t/min
D en mm
(Formule d'avant projet)
Epaisseur d'une conduite forcée
Attention : la formule suivante ne vérifie pas toutes les contraintes
auxquelles sont soumises les conduites et notamment:
Les flexions longitudinale et latérale
L'apparition fortuite d'une forte dépression intérieure (vide)
La formule donne donc une valeur indicative qui demande d'autres vérifications
Cette formule pour un métal homogène sans trous de perçage (rivets..) est
e =10 * P * D / (2 * R)
Attention aux unités qui ne sont pas homogènes pour des raisons de pratique
courante
e est en mm avec minimum de 1
P est la pression max (y compris coups de bélier)
en bars
D est le diamètre en mètres .
R est le taux de travail en daN/mm2 du métal généralement pris au 1/5 de la
charge de rupture
soit pour l'acier soudé 8 daN/mm2
Parlons
un peu du Choc
Retour page
d'accueil
Notes memo
Dans notre présentation nous utilisons presque exclusivement les unités du
système international S.I.
Les unités fondamentales sont entre autres
Le Kilo pour la masse
Le mètre pour la longueur
La seconde pour le temps
Le Newton pour la force ou le poids
Une masse de 1 kg a un poids de 9.81 N sur notre
planète.
1 Newton * 1 mètre = 1 joule unité de travail ou énergie
C'est le travail d'une force de 1 Newton se déplaçant de 1 m dans sa
propre direction
1 joule/sec = 1 watt
1 Wh =3600
joules
1 Kw= 1000 W = 1000 joules/sec
1 Kwh= 1000 Wh = 3600000 joules = 861244 petites calories
= 861 Kcalorie
1 Kcalorie= 4180 joules
1 Kcalorie permet d'élever de 1° C la température d'une masse d'eau de 1
kilo
Ainsi pour réchauffer de 20° à 70° l'eau d'un chauffe eau de 150 litres il
faut lui apporter
150 * 50 =7500 Kcalories ce qui correspond à 8.7 Kwh (1 Kw pendant 9 heures
env.)
Attention à ne pas confondre calorie et Kcalorie , car le langage courant
désigne souvent par calorie la Kcalorie que l'on appelait encore auparavant grande
calorie.
Ainsi quand on parle de calories pour les besoins énergétiques d'un être
humain , ou pour les déperditions thermiques d'une pièce , il s'agit de
Kcalories.
1 kilogrammètre (anciennes unités) = 9.81 joules
1 kilogrammètre/seconde (anciennes unités) = 9.81 watts
Bien que commode à utiliser , la Thermie
n'est pas une unité légale elle vaut 1000 Kcalories , elle est très utilisée
par les pétroliers.
Unité de pression
Pascal (Pa) = 1 Newton/m2
Le Pascal est une unité très petite : 1 atmosphère = 1 Bar
= 100000 Pascals
Unité de Couple
1 mètre * 1 Newton = 1 Métre-Newton
(mN) : Couple
Le Couple * par la vitesse angulaire donne la puissance
Unités spécifiques de l'eau
r
: masse en kg de 1 m3 d'eau soit 1000
v
: poids
en newtons de 1 m3 d'eau soit 9810 (souvent arrondi à 10000)
g : accélération de la pesanteur terrestre : 9.81 m/s/s
Retour page
d'accueil
a b c d e g h j i b k l m n o p q r s t
u v w x y z