ROUE VANNE

Pour commencer , nous allons simplifier le problème en nous plaçant dans le cas de 2 plans d'eau assez étendus , voisins , mais séparés par une dénivellation de quelques mètres
Entre les 2 plans on creuse un canal rectangulaire qui au lieu d'être fermé par une vanne sera barré par une roue vanne .

L'image ci dessous représente une roue de ce type , une roue Sagebien qui a des caractéristiques très particulières.
Si la roue est arrêtée , l'eau ne passe pas , fuites mises à part bien entendu.
Ce type d'installation demande une construction soignée et précise ! Le jeu entre les bajoyers et la roue doit être aussi faible que posible ; de même entre le coursier et la roue


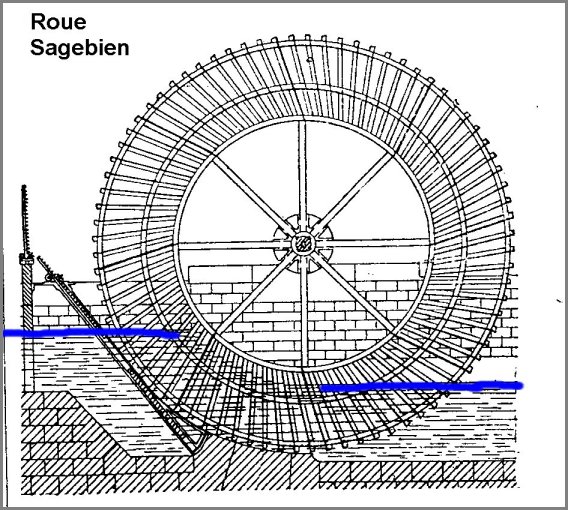
cette roue a un grand nombre de pales .

Le niveau supérieur est H1 , le niveau inférieur H2 , la différence de niveau est H.
Quand la première pale ferme le contact avec le niveau amont , le niveau d'eau entre les pales successives va baisser progressivement, en partant du principe de la conservation du volume introduit
Chaque pale reçoit une poussée fonction de la différence des hauteurs d'eau
La totalité des poussées correspond à la hauteur totale H
Pendant toute cette période les aubes sont hydraulique-ment isolées de l'amont et de l'aval

La pale qui va quitter le coursier et se trouver toute entière dans le bief aval , va se "vider" en fait  elle perd toute sa pression restante et sera soumise à la pression basse H2.
Elle se vide par  un écoulement  à  vitesse très lente.
C'est grâce à cette lenteur que la perte d'énergie est minimalisée vu notamment l'absence de tourbillons

Le dessin schématique ci dessous donne une explication qui se voudrait encore plus simple du fonctionnement.

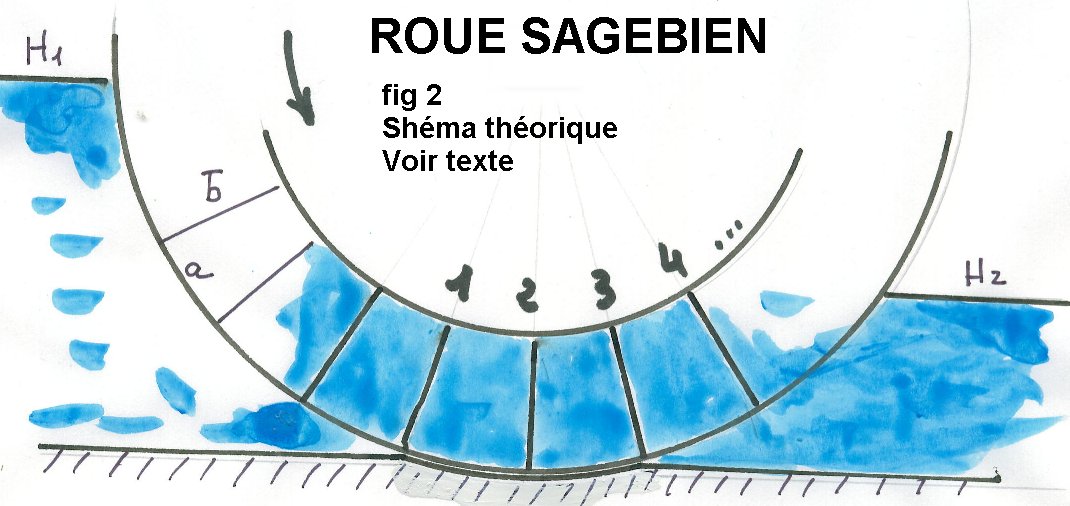
Tant que la pale 3 n'a pas quitté le coursier , toute l'eau contenue entre 2 et 3 est à la pression due au niveau H1
Dès qu'elle commence à le quitter , le volume est mis en communication avec le niveau aval.

La pression tombe aussitôt.

La pale 2 est soumise à une force due à la différence de pression.
Cette explication est ultra simpliste

Une étude bien plus avancée est donnée dans une autre page

Pendant cette période un effort pratiquement constant a été exercé sur cette pale 

Cet effort a produit un couple qui fait tourner la roue.
Par ailleurs un volume d'eau est passé de l'amont vers l'aval.
Ce volume est celui contenu entre 2 pales. La masse d'eau  correspondante M de poids  M * g   a perdu une énergie M *g * H.
Les pertes étant surtout dues aux fuites , le rendement peut être trs élevé

On pressent qu'il y aura une vitesse optimale ou l'énergie perdue sera égale à celle récupérée par la roue. Du moins s'il n'y a pas de pertes.
En fait , la roue vanne a un bon rendement. Elle se comporte comme un "compteur d'eau" . S'il n'y a pas de turbulences , pas de tourbillons , l'eau s'écoule dans des conditions "idéales".

A contrario , si on laisse la roue libre de toute résistance mécanique , elle prendra une vitesses élevée et le régime sera ultra tourbillonnaire.
Tout se passera comme si la roue n'existait pas et un débit énorme sera gaspillé en pure perte.

CALCULS POUR CETTE ROUE
Nous avons vu que tout régime tourbillonnaire doit être évité , donc la vitesse doit être  très lente.
La roue sera très grande .
Essayons , à titre de comparaison de déterminer une roue Sagebien pour notre roue d'exemple 
Tout d'abord , notre installation hydraulique devra subir des transformations: obligation de construire un canal d'amenée très soigné comme dit ci dessus et de creuser profondément le canal de fuite , au moins sur une certaine longueur.
De plus , nous voyons immédiatement que le rayon de la roue sera supérieur à la hauteur de chute , compte tenu de la nécessité de mettre le moyeu de la roue au dessus des maçonneries.
Comme notre chute est de 5.20 m , nous prendrons un diamètre de 22 mètres.
En prenant une vitesse circonférentielle faible (0.6 m/s) , la vitesse de rotation sera de 60*0.6/(pi*22)  = 0.52 T/min arrondi à 0.5
Prenons un grand nombre de pales , soit 80 comme dans la figure du haut de la page .
En 1 seconde , la roue a tourné de 360 * 0.5 / 60 = 3 degrés.
Or le pas des pales est 4.5 degrés.
Notre débit était de 360 l/s
Il faut donc que le volume entre 2 pales soit 360 * 4.5 / 3 = 540 litres.

Les dimensions de la surface utile entre 2 pales sont assimilables à un rectangle , avec (voir le dessin 2 de cette page)

a = 0.86 m soit 8.6 dm
b=   D/5 (env .) = 22/5 =4.4 m soit 44 dm
soit une surface a * b de 378 dm2
On en déduit la largeur de la roue : 540 / 378 =1.428 dm ou 0.14 m  , roue donc très étroite et très irréelle !

On peut facilement  calculer le volume spatial des roues
L 'encombrement de la roue Sagebien est de 53 m3
Celui de la roue en dessus était de 19 m3

Et les poids sont grosso modo en proportion des volumes.
Le lecteur en déduira les cas ou une roue Sagebien est souhaitable et verra que cette roue s'applique à de très grands débits sous de basses chutes .
Dans notre calcul , en ne changeant que le débit que l'on multiplies par 10 , la roue a une largeur qui passe à  1.40 m .

Avec une puissance de 249 CV

La roue de l'ingénieur Alphonse Sagebien, d'après un brevet déposé en 1858, est une roue de côté dont les aubes sont planes, profondes et encastrées, avec un très faible jeu entre les murs du coursier. Dans la seconde moitié du XIXème siècle, cet ingénieur a installé dans notre département plusieurs de ces roues. Elles représentaient alors le moteur hydraulique le plus élaboré. L'admission de l'eau se fait par une vanne tangente à la roue. Le rendement est très élevé : il peut atteindre jusqu'à 90 %.


Retour page d'accueil