TYPES PRINCIPAUX DE ROUES

Nous commençons par la roue au dessus  

    UN PEU DE CALCULS

On remarque que l'eau arrive sur la roue à une faible vitesse . Une  petite  partie de l'énergie de vitesse est récupérée par l'aube. 
Pour cette raison il faut au moins que le profil de l'aube doit être établi pour une entrée sans choc  : voir ci après .

En reprenant la figure de la roue au dessus nous allons nous fixer des caractéristiques pour rendre notre travail plus clair .

Nous utilisons les paramètres suivants :
Débit  360 litres /seconde
Hauteur de chute  5.20 mètres

Puissance théorique :  24.9     CV  ou  18364  watts  voir (formule puissance)
Pour aménager la tête d'eau nous devons nous réserver une hauteur de 0.70 
Nous devons faire un petit calcul par tâtonnements pour vérifier que notre tête d'eau nous fournit facilement le débit demandé.

La hauteur d'eau dans le petit canal sera de 0.60 mètres ; la vanne sera levée de 0.14 mètres .
Largeur du canal  1.2  mètre
Le débit sera de 360 litres / seconde (voir  formule vanne)
On calculera facilement les 2 points suivants :
La vitesse de l'eau est  3.43 m/sec
La hauteur du jet d'eau est de 8.74 cm soit un coefficient de contraction de 0.62 valeur classique

Diamètre de la roue  4.50  mètres
Largeur de roue 1.2  mètre
Nombre d'augets :48

Hauteur de la couronne : 0.4  mètres
Volume de la couronne = 6182  litres
Volume d'un auget   6182 / 48 =129 litres
Volume utile de remplissage : 60   litres soit env. 50%
Le remplissage avec notre débit suppose que 6 augets défilent en 1 seconde , ce qui correspond à une vitesse de rotation N de 7.5  tours par minute .

La vitesse circonférentielle est de 1.76 m/sec 
Cette vitesse est acceptable 
Des vitesses trop grandes (3 m/sec) entraînent une perte d'eau par éjection centrifuge prématurée.

Le poids de l'eau dans 20 augets actifs grosso modo , est équivalent à une force de 1200 * 9.81 = 11772  Newtons  appliquée au centre de gravité situé à environ 1.40  mètres du centre de la roue .
.
Le couple est 11772 * 1.40 =16481  mètres-Newton
Et la puissance (P =couple * vitesse angulaire)
P = 16481 * 2 * pi * N/60  soit  12944  watts
Cette puissance est inférieure à la valeur ci dessus du fait que la roue a un diamètre inférieur à la hauteur de chute car l'alimentation avec tête d'eau. nous  fait perdre 46 cm

Si on double la largeur de la roue les augets seront deux fois plus volumineux , le couple sera doublé mais la vitesse sera divisée par 2 à cause du temps de remplissage et la puissance sera inchangée si le débit ne change pas .

(Cependant on peut conserver la vitesse si le doublement de largeur correspond au doublement de largeur du canal d'amenée et au doublement du débit , la puissance est alors doublée)


Il faut aussi tenir compte des augets inactifs car déjà vidés ou presque
Si tous les augets étaient actifs la puissance serait augmentée de 20%
En tenant compte de ces divers facteurs on retrouve la puissance théorique de 3395 watts.

Le dessin ci contre montre une roue en dessus en bois fabriquée dans les Ardennes et en service depuis 1992 alimentant en électricité 2 gîtes ruraux situés en forêt des Ardennes Belge et ne pouvant être raccordés au réseau général.






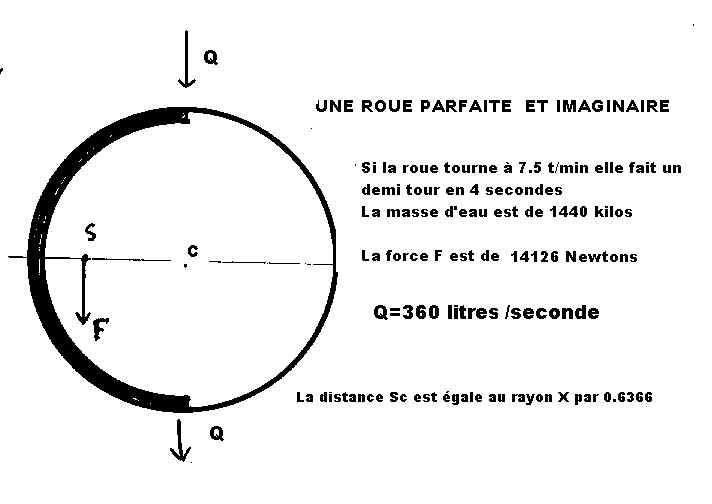
Figuration d'une roue parfaite 
Cette roue , totalement imaginaire et irréalisable va nous montrer ensuite  les défauts de la roue réelle.
Notre roue fictive a un diamètre égal a la hauteur de chute ., soit 5.20  mètres  dans notre exemple

Il n'y a aucune perte de hauteur. d'eau 
Le nombre d'augets est aussi grand que possible et tend vers l'infini.....
Tous les augets gardent leur eau depuis le haut jusqu'en bas.
La roue tourne à la même vitesse (7.5 T/min) seconde 
 les augets actifs (50 %) contiennent en tout 1440  litres d'eau.
Une moitié de la roue peut presque être assimilée à une cercle d'épaisseur nulle mais pesant de toute la masse d'eau
Il s'agit bien entendu d'une vue totalement théorique

Le centre de gravité de ce cercle est situé à une distance du centre égale au rayon * par 0.6366
Ce dernier coefficient est connu dans les cours de mécanique classique.
La totalité des forces de gravité  appliquées à la roue est équivalent à une force unique , verticale , passant par ce centre de gravité
La masse d'eau emprisonnée dans le demi cercle est égal au débit * par le temps mis par la roue pour faire un demi tour , soit 3 secondes dans notre cas particulier.

Cette masse d'eau est de 1440  kilos
La force F est de 14126 Newtons 

Le couple est 14126 * 2.6 *0.6366 = 23383 mètres newton

La puissance est couple * vitesse angulaire soit 
    P=   23383* 2 * p * 7.5 / 60 =18365  watts





Nous retrouvons bien notre puissance totale .

Pour plus de renseignements voir le formulaire

Analyse des pertes (dans le cas réel)

Nous avons vu plus haut l'influence néfaste de l'alimentation avec tête d'eau qui nous fait perdre 0.70 de  hauteur qui n'est   récupérée  qu' à 40 % environ 

Mais ce n ' est pas tout 
Il faut considérer la situation énergétique de l'eau contenue dans cet auget.
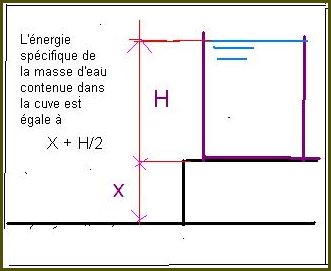
Considérons d'abord une cuve remplie d'eau située sur un monticule

La hauteur du est X  , celle de la cuve est H
Appelons Ep l' énergie par unité de poids ; cette valeur est assimilable à une hauteur
Pour l'eau de notre cuve , l'énergie n'est pas X + H , mais X + H/2

 
Considérons l'auget qui vient de se remplir .Nous avons noté que ce remplissage , effectué en douceur grâce à un tracé correct des aubes , a  pu procurer une petite addition de couple moteur 

Par ailleurs il faut examiner ce qui se passe au dessous du niveau médian , dans le coursier . Ce dernier est bien destiné à empêcher l'eau de s'échapper , mais au fur et à mesure que les aubes descendent le poids de l'eau quelles contiennent diminue du fait des pertes  car l'étanchéité ne peut être parfaite.

En résumé :
Sans tenir compte des pertes d'eau par débordement , le rendement hydraulique de notre roue ne saurait dépasser 2594 / 3395 soit 76.4  % dans les meilleures conditions de réglage du débit et de la vitesse .

Il faut ajouter les pertes d'eau et les pertes mécaniques diverses
En fait le rendement sera inférieur comme on verra ci après

Nous traitons dans une autre page le Tracé des aubes

Compléments touchant au   Rendement

A partir d'une position de l'aube au dessous d'un angle de 30° environ sous l'horizontale , l'aube commence à se vider ; le coursier contribue à conserver l'eau mais avec des pertes par frottement.
Notre dessin montre que le nombre d'aubes actives est sensiblement 18 au maximum soit 18/24 = 0.75
De plus un coefficient de réduction doit et re appliqué du fait que le centre de gravité des masses d'eau dans les aubes n'est pas sur la circonférence externe mais sur un courbe plus intérieure ;ce coefficient est d'environ 0.96 
Cette valeur est applicable à tout type de roue de ce genre
Le rendement ne saurait dépasser ainsi 75 * 0.96 =72 %
Il faut tenir compte de plus de la perte de hauteur due à la tête d'eau soit au moins 10% dont on peut espérer une récupération de 4% environ par l'aube (surtout si bien profilée , courbes au lieu de droites) 
S'il y a  un coursier supérieur pour guider la lame d'eau entrante , il faut tenir compte de la perte de charge dans ce coursier
Avec  les valeurs données plus haut (360 l/s, largeur 1.2 ,  épaisseur du jet 0.87 ) et en choisissant une paroi lisse la perte de charge est de 56 mm/m
Cette valeur peut être renvoyée par mon logiciel 

Ainsi le rendement calculé de notre roue ne saurait dépasser 64 à 67% 
Toute allégation autre que l'on pourrait trouver dans des ouvrages ne peut être défendable.
Le rendement réel est encore inférieur .
Et pourtant la roue au dessus reste une des meilleures 

Calculs constructifs

Il faut encore calculer certains organes , comme la structure du "squelette" savoir les membrures et les couronnes.
Ces organes se calculent par la résistance des matériaux , compte tenu des forces appliquées.
Il faut cependant ne pas construire trop léger étant donné les incidents possible es exploitation

L'arbre de la roue sera calculé par la formule simple de la résistance des matériaux
En prenant 15 CV comme puissance utile la formule nous donne un diamètre d'arbre de 120 à 150 mm ce qui est assez considérable


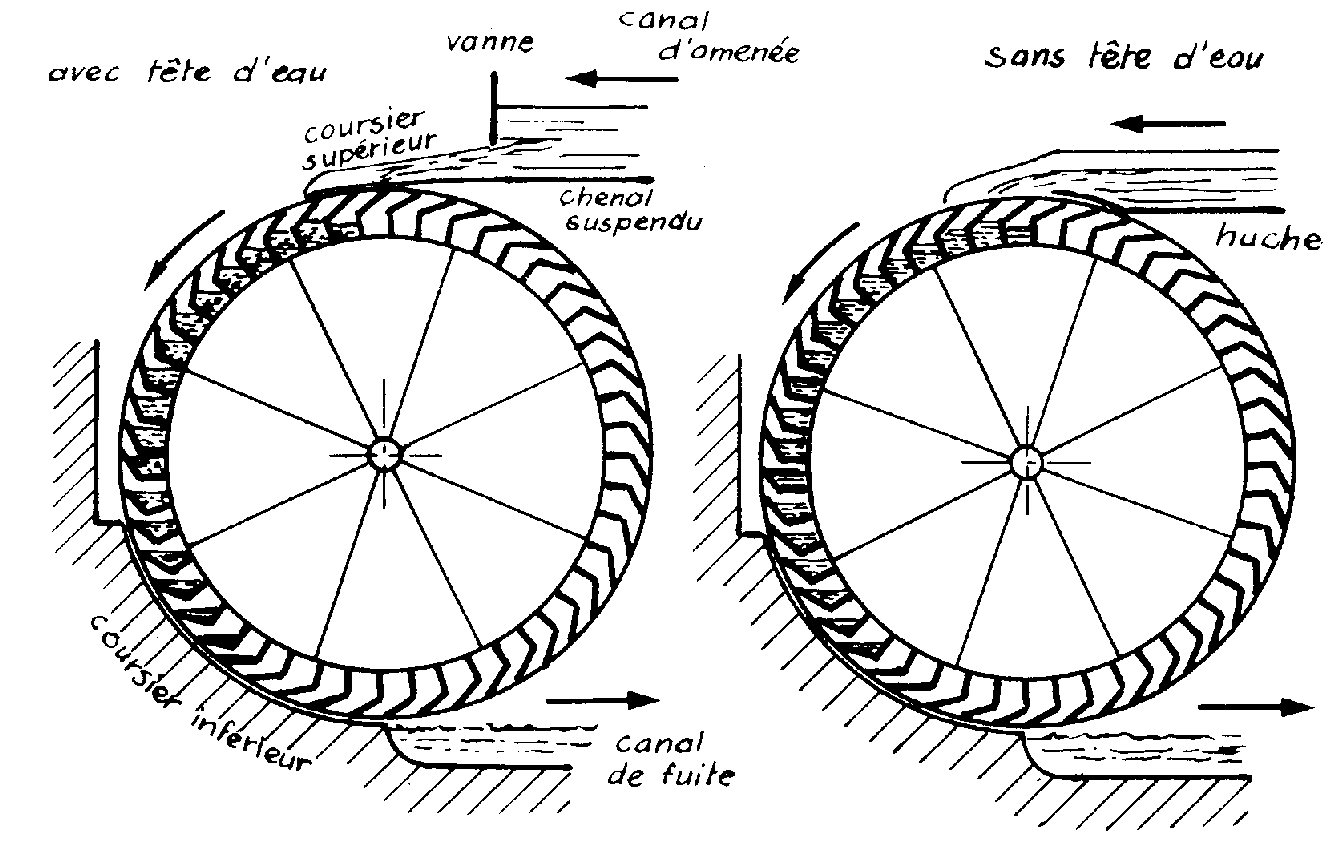
Cas d'une admission sans tête d'eau

Le croquis ci dessous montre la différence entre 1es 2 types de ces roues
Dans  la roue sans tête , l'eau tombe dans la roue avec une vitesse très faible , comme un déversoir.

Il en résulte que l'énergie cinétique est bien moindre et que l'eau agit presque uniquement par son poids dès son admission.
Pour cette raison , la roue tournera moins vite
On considérera la lame déversante comme une lame de déversoir et nous admettrons la formule :

V= 0.41 * racine( 2 * g * hl)
hl étant l'épaisseur de la lame. (m ,m/s)

Ainsi la vitesse de l'eau sera de 0.41 m/s pour une lame de 10 cm et de 1 m/s pour une lame de  30 cm
Cette variation de vitesse se répercute sur celle de la roue qui est plus faible



Dans ce cas le diamètre de la roue peut pratiquement être égal à la hauteur de chute.
Il en résulte une augmentation sensible de la puissance donc du  rendement de l'installation.

Bien entendu la roue géométriquement semblable a toutes ses dimensions augmentées
Désignons par a le coefficient d'augmentation du diamètre de la roue ; le tableau ci dessous nous indique les coefficients de variation des différents paramètres.

Dans notre exemple nous aurions a= 1.2

Comme la vitesse de la roue est divisée par 1.44 , on peut grosso modo conserver le même tracé des augets si la vitesse de l'eau est réduite dans les mêmes proportions .
Dans le premier cas il y avait une vanne chargée sou 0.46 mètres . dans le second cas la charge sera 4 fois plus faible soit 11.5 cm ce qui correspond à une une lame déversante  et satisfait à notre géométrie.

Les augets défilent à raison de 7 augets par seconde au lieu de 10 .
Le rendement est très augmenté.

Il faut remarquer que l'admission par le dessus peut revêtir différentes configurations.
ainsi on peut avoir un canal d'amenée ou l'eau prend de la vitesse grâce à sa pente ; celle ci cependant ne doit pas être trop grande. Ainsi la vanne de tête est supprimée et remplacée par un seuil faisant office de déversoir noyé , suivi lui même du canal qui vient d'être mentionné.

Ce canal peut lui même se terminer par un déflecteur qui modifie   l'orientation de la  vitesse l'eau comme on le  souhaite , dans certaines limites cependant.

Roues de poitrine et roues de coté

La roue en dessus a l'inconvénient d'imposer une déviation de 180 degrés à l'écoulement du courant.
D'autre roues ont donc été imaginées , ou l'admission de l'eau se fait plus bas que le sommet de la roue .
Le sens du courant n'est pas inversé entre l'arrivée et le canal de fuite.
Ces roues peuvent avoir un diamètre bien supérieur à la hauteur de chute (jusqu'au  double environ) ; compte tenu de ce qui est expliqué dans  le Tracé des aubes  , la vitesse de la roue sera réduite dans les mêmes proportions .
J'ai déjà signalé de problème dans la page générale
Le respect du triangle des vitesses impose un guidage des filets d'eau  à l'entrée et certaines roues de poitrine avaient un véritable distributeur orientable commandé par la vanne d'admission. La figure ci dessous en donne un exemple sommaire


Il faut noter que dans ces roues , ainsi que dans la roue de coté qui est assez semblable mais sans ce vannage complexe et avec une admission à mi hauteur de la roue ou même plus bas , le coursier inférieur a une importance primordiale : le coursier est le seul organe qui permette à l'eau de rester dans les augets , aussi la construction doit elle en être particulièrement soignée.
Les roues de coté peuvent être comme les roues en dessus , avec ou sans tête d'eau.
Si l'admission de l'eau se fait assez bas il est cependant possible de dessiner les augets pour que ceux ci ne se vident pas trop vite et l'influence du coursier est diminuée
La roue devient d'un diamètre très supérieur à la hauteur de chute , aussi , cette disposition n'est applicable qu'à de bases chutes de 1 à 2 m 
Dans ce dernier cas on peut s'attendre à d'assez bons rendements    avec une construction très fine , ainsi les industriels de la vallée de la Thur (Alsace) ont ils amené ces roues à un degré de perfection assez élevé , juste avant l'arrivée des premières turbines ,  à la fin du 19ème siècle.

Pour la construction de la roue , voir aussi la nouvelle page

Comment varie le débit par mètre de largeur en fonction de la hauteur de chute .

Retour
Note

L'énergie de vitesse par litre d'eau est égale à  g x dh , dh étant la différence de hauteur entre le plan d'eau supérieur et le point de rencontre entre l'eau et la roue.

La vitesse de l'eau ne peut être évidemment nulle .
Elle est égale à racine carrée de (2 * g * dh) soit en écriture mathématique :
avec z=dh
Ainsi pour dh = 0.5 mètres
     v = 3.13 m/seconde
 L'énergie théorique est de 4.9 watts par litre  

Retour