ETUDE DE LA ROUE DE COTE

L'image ci dessous est la reproduction d'un excellent dessin donné par Monsieur Bazard dans un ouvrage datant de 1918 (Cours de Mécanique , tome 3, Albin Michel)
Cette roue ayant des aubes remontantes , est en fait une roue modifiée de type Bélanger
Cette particularité ne change que très peu  au texte ci dessous



La roue sans tête d'eau possède une fonçure et les pales sont tenues par des coyaux visibles sur le dessin
les pales sont en 2 pièces (ligne brisée) , mais cette disposition (Roue bélanger ) n'est pas générale ni obligatoire
Souvent les pales sont plates et comme nous le verrons elle sont radiales
La fonçure est percée pour chaque auget de quelques trous dans la partie la plus haute pour permettre l'évacuation de l'air
L'axe de la roue est au dessus du niveau amont
Cette disposition permet d'avoir de grandes roues avec de faibles chutes

Réglage du débit

L'eau est admise avec une vanne plongeante oblique  , comme pour la roue Sagebien
On suppose la vitesse de l'eau négligeable  à l'infini amont
L'eau arrive donc par dessus la vanne qui se comporte comme un déversoir

La vitesse de l'eau est  faible ; elle est donnée par la formule très approchée

V1 = 0.7 * racine (2gh) 
h étant non la hauteur de chute mais la dénivellation entre le plan d'eau amont éloigné et le dessus de la vanne

On aurait ainsi une vitesse de 1.40 m/s pour h= 0.10 m et 2.80 pour h = 0.40 m
On comprend que cette roue va mal s'adapter à  de fortes variations de débit
Pour les valeurs indiquées , les débits sont respectivement de 55 l/s et de 450 l/s par mètre de largeur , ces valeurs sont beaucoup trop différentes
On devra rester entre des débits variant seulement du simple au double
Par exemple , de 100 à 200 l/s correspondant à des valeurs de h allant de 0.14 à 0.23 m
Pour 200 l/s et 1.5 m de chute la puissance est d'environ 3 Cv par mètre de largeur
Ainsi avec 1.50 m de chute la roue aurait , comme le dessin nous le laisse mesurer , environ 4.60 m de diamètre
Si elle a 2 m  de largeur , la puissance sera de 6 Cv
Les puissances sont faibles au regard des dimensions.

Rôle primordial du coursier et des bajoyers
L'eau est maintenue dans la roue en plus des aubes et de la fonçure uniquement  par le coursier cylindrique et les bajoyers, organes qui se doivent donc d'être aussi parfaits que possible
remarquer sur le dessin le sabot qui termine le haut du coursier
Cette pièce était généralement en fonte

Cette disposition est différente de la roue au dessus dans laquelle le coursier n'a qu'un rôle complémentaire voire facultatif.

Les fuites sont une cause importante de perte de rendement

Détail de l'admission de l'eau
On remarque sur la figure que la vanne est pour ainsi dire collée à la roue
Cette disposition est importante pour avoir le moins de perte de chute possible
L 'énergie correspondant à  la mise en vitesse de l'eau est compte tenu de la formule ci dessus
égale à  V1^2 / (2g)  = 0.7  h

En fait et comme une partie de l'eau tombe un peu plus bas nous pouvons admettre une perte au moins égale   à h


La vitesse périphérique de la roue U1 est en général de 0.85 V1 soit pour notre exemple 1.80 m/s
(On choisit une vitesse relativement élevée pour diminuer les fuites )
Pour une roue de 4.60 , la vitesse de rotation est de 7.5 T/min
Cette vitesse est élevée compte tenu de la faible hauteur de chute

L'eau a alors une vitesse nulle par rapport à la roue , mais égale à U1^2 /(2g) par rapport a des repères fixes
Elle a perdu (V1^2 - U1^2) /(2g) 

Triangle des vitesses à l'entrée

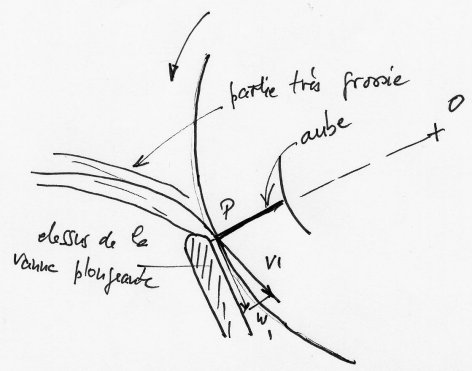
Le dessin montre l'arrivée sur la roue d'un mince filet d'eau
On prend un filet mince pour la démonstration et encore on ne considère que le filet moyen
La vitesse V1 est celle déjà vue , au moins approximativement, le vecteur correspondant coupe le cercle en P sous un angle a
La vitesse U1 est déterminée par celle de la rotation
On a constaté que de bonnes conditions étaient satisfaites si U1 = V1 * cos(a)
Le coefficient de vitesse est environ le double de celui de la roue au dessus
Le triangle est alors rectangle

Si a =30° , valeur usuelle , alors U1 = V1 / cos(30) =0.87 V1 et W1 = 0.5 V1

 La vitesse  W1 est alors parallèle à la ligne OP
Les aubes sont radiales , sauf brisure comme déjà vu
C'est la vitesse W1 qui permet l'entrée de l'eau
Il faut donc vérifier par un calcul élémentaire que cette vitesse est suffisante pour remplir les augets
Avec W1 = 0 ; la roue tournant vite ne peut se remplir , elle forme barrage

Le dessin suppose une approche très étroite entre la roue et le dessus de la vanne plongeante et de tout façon il est impossible de ne pas perdre une petite hauteur de chute supplémentaire car la vanne ne peut avoir une épaisseur nulle

Ceci revient à augmenter un peu la valeur de h

Sortie de l'eau

L'eau en quittant la roue emporte  sa  vitesse d'entraînement qui est "perdue"
La nouvelle perte est U1^2 /(2g)
Au total la perte vaut donc  V1^2 / (2g) , c'est à dire la totalité de l'énergie cinétique dont aucune partie n'a été transformée en énergie mécanique
Une explication plus analytique de la perte d'énergie cinétique est donnée par ailleurs

A ce stade , le rendement est (H-h)/H , soit 0.84 pour l'exemple ci-dessus ( H = 1.5 m , h = 0.23 pour 200l/s et la valeur de V1 est 2.12 m/s
En fait h doit légèrement majoré , comme dit quelques lignes plus haut

Une roue de coté de 5.20 de diamètre dans dans la Sarthe , 2.2 de largeur , 1.30 de chute , 7 kw de puissance utile

Soins à la construction
Compte tenu de ce que nous venons de voir , la roue de coté ne vaut que par le soin apporté à son étanchéité et à la précision des organes d'admission .
On peut remplacer la vanne plongeante par une tête d'eau , mais la perte d'énergie cinétique est encore plus importante et donc le rendement moins bon
La roue avec tête par contre s'accommode bien mieux des variations du niveau amont et des variations de débit

EXEMPLE  DE CALCUL PAR LE LOGICIEL

Retour