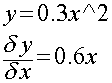TRACE DES AUBES ET
AUGETS
Aube : Surface soumise à l'action de
l'eau ou servant de cloison étanche
Auget ; "Poche" (nom ancien d'ailleurs) qui retient prisonnier un
certain volume d'eau
La terminologie aubes ou augets est donc assez
subtile
On désignera par aube toute surface "travaillée" par l'énergie de
l'eau.
Les augets supposent des roues foncées : la fonçure ferme la roue du
coté intérieur ; parfois elle est aérée pour que l'air n'empêche pas le remplissage
(cas des roues de poitrine et de coté)
Les augets ont un double rôle
Offrir à l'eau une surface bien présentée (partie aube ,
triangle des vitesses)
Conserver le maximum de volume d'eau le plus
longtemps possible

Bien que le but de la roue est de récupérer
la force de gravité , nous dirons quelques mots sur l'admission de l'eau et la récupération
d'énergie cinétique : nous verrons que cette récupération est assez faible
Les roues peuvent être avec '( fig ) ou sans
tête d'eau
Ces dernières ont une géométrie assez
semblable , mais l'eau arrive moins vite par déversement , les roues seront
plus encombrantes et moins rapides mais leur rendement sera meilleur.
Dans cette page nous parlons uniquement des roues avec tête
Le triangle des vitesses
Il est indispensable de bien connaître ce
triangle
Certes , il est bien moins important dans les cas d'une roue que dans celui
d'une turbine , dans laquelle il agit directement sur la totalité rendement
Cependant il importe que l'eau pénètre dans la roue sans créer une perturbation (choc)
qui pourrait faire gicler l'eau à l'extérieur en pure perte par exemple ou
causer des tourbillons et du bruit et perdre quelques pointe de rendement .
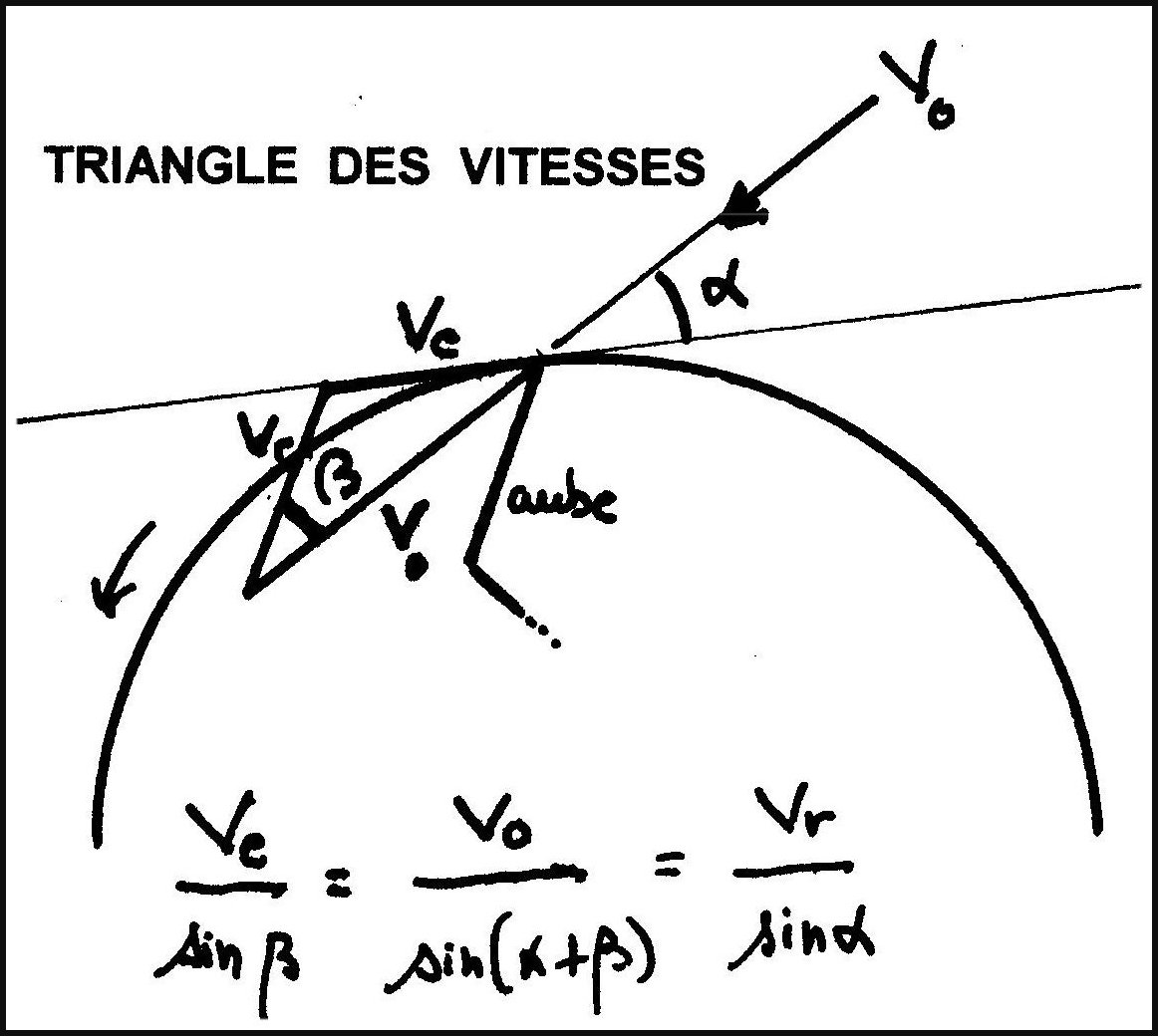 Désignons (fig.) par Vo la vitesse de l'eau qui arrive , a
l'angle de cette vitesses avec la
circonférence externe de la roue , Ve la vitesse périphérique , Vr la
vitesses relative
Désignons (fig.) par Vo la vitesse de l'eau qui arrive , a
l'angle de cette vitesses avec la
circonférence externe de la roue , Ve la vitesse périphérique , Vr la
vitesses relative
Nous désignerons par m le rapport Ve/Vo
Le développement des équations de base indiquées sur la figure conduit à :
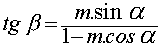
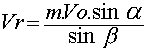
L' aube fait avec la circonférence un angle
d = a + b
Cet angle est lui aussi important
S'il n'y a pas de petit coursier la veine d'eau qui sort sous la vanne a une ligne moyenne
qui est celle de la parabole
Il y a intérêt à ce que le jet
rencontre la roue le plus haut possible , car toute hauteur perdue est
pratiquement.... perdue
S'il y a un petit coursier c'est lui qui déterminera plus ou miens bien notre angle a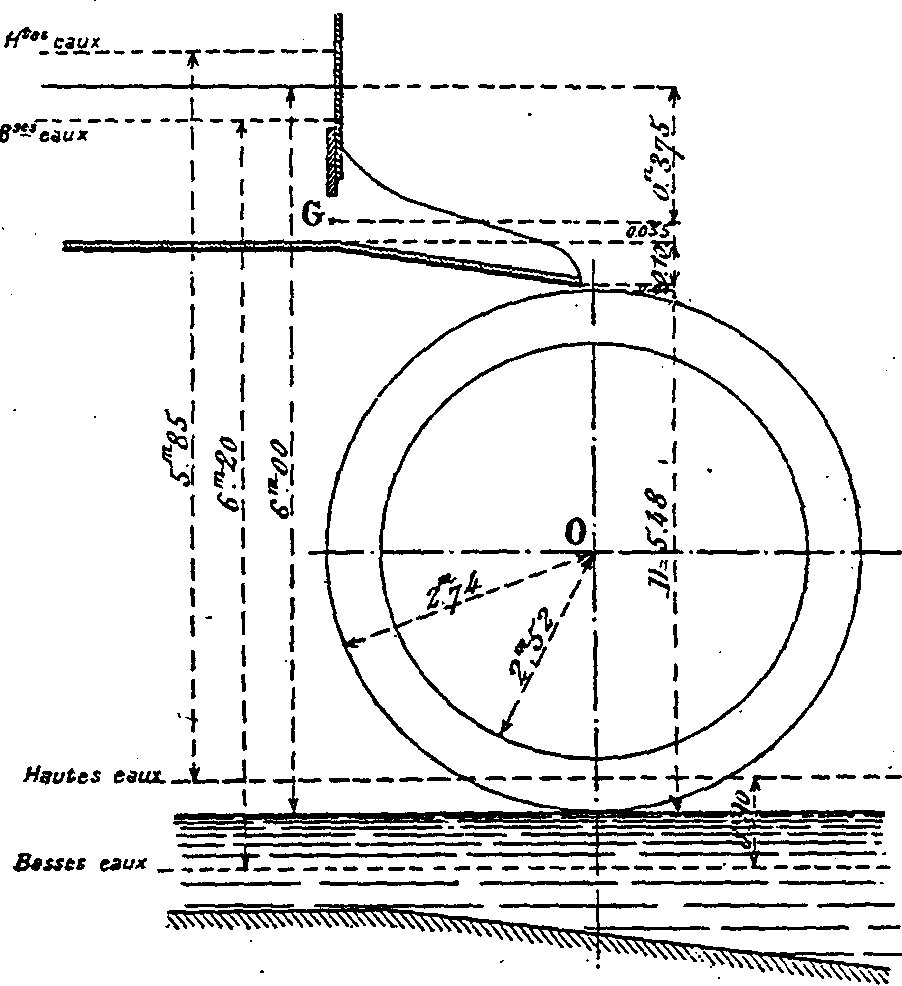 (voir ci après)
(voir ci après)
Ce coursier doit être aussi court que possible car il ne faut pas s'imaginer
que l'eau s'accélère en descendant le long de ce skip.
L'image ci contre est extraite d'un manuel écrit en 1918 par Monsieur BAZARD
Les aubes
La construction en bois a conduit aux aubes
en 2 parties de longueur plus ou moins égale d'une "ligne" brisée .
Le but essentiel est de loger beaucoup d'eau et de la garder le plus longtemps
possible
On a fait des aubes courbes en tôle : poches plus grandes et récupération
d'énergie cinétique améliorée
Les connaisseurs penseront au théorème d'Euler....qui là joue un peu
Le long de la première partie , il n'y a
aucune récupération d'énergie cinétique
La brisure , qui constitue une déviation ,
apporte une force qui augmente un peu le couple mais cet effet est vite annulé
quand l'aube se remplit , à un taux qui ne devrait pas excéder 50% en
général.
L'eau arrêtée a perdu sa vitesse relative et ne conserve que sa vitesse
rotatoire , mais comme celle ci sera aussi la vitesse de sortie le bénéfice
est nul.
Problèmes concernant l'admission de l'eau
Nombre d'augets
En fait d est
assez voisin de 2
a
Si l'angle a est trop petit ; l'eau ne pourra pas entrer
convenablement dans la roue
Le jet coupe le cercle externe selon un arc de ce cercle.
Si l'arc est petit on peut l'assimiler à une droite
Nous avons la relation
épaisseur du jet entrée = arc * sin(a
)
Dans la roue , comme la vitesse relative est plus faible , l'épaisseur de la
lame d'eau est plus grande
épaisseur du jet dans la roue = arc * sin(a+b
)= arc * sin(d )
Ceci bien entendu avant que l'eau ne s'écrase dans le fond de l'auget.
Ces relations faciles à démontrer ne sont plus valable si l'arc coupé et*st
trop grand(par rapport au diamètre de la roue évidemment)
Le nombre d' augets sera fonction de ces conditions.
Dans le cas d'aubes en bois , un grand nombre d'augets réduit le volume utile
de la couronne
En général on prend comme pas des augets l'arc + l'épaisseur de l'aube
+ 2/1000 du diamètre
Par ailleurs pour que l'auget ait un volume aussi grand que possible , il faut
que d
soit petit
On prend généralement pour a
une valeur de 15 à 20 °
Le réglage pose des problèmes
1 Sans coursier
Dans la figure TRACE DES AUBES en haut de cette page , on laisse l'eau suivre sa
ligne parabolique.
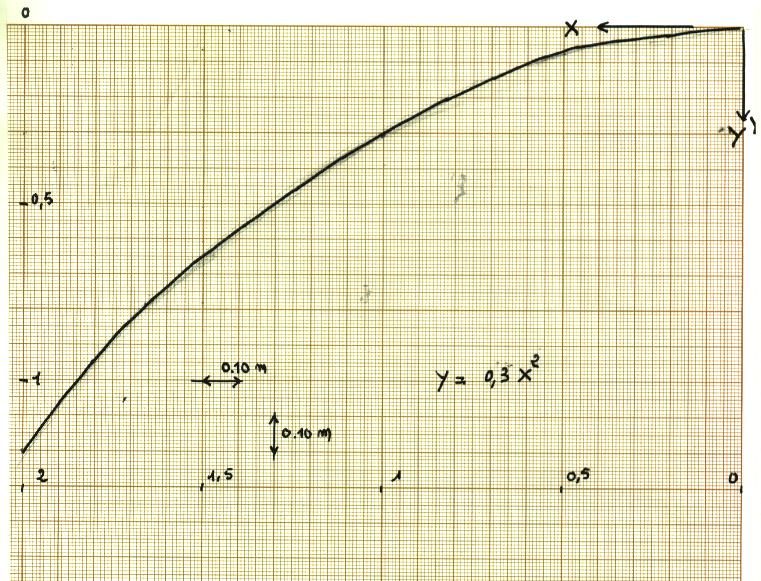
La courbe dépend de la
hauteur h de chute de la tête d'eau
Le diagramme ci dessus a été tracé pour une hauteur h sur la vanne du
petit canal de 0.60 m
Pour des valeurs différentes on prendra
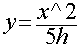
Il faut ensuite trouver le point du diagramme correspondant à un angle de 16°
si on choisit cette valeur.
La tangente de cet angle est 0.286
Comme dans ce diagramme nous avons déterminé la fonction y(x) et donc sa
dérivée :
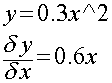
Nous aurons 0.286 = 0.6 x soit x = 0.477 m pour h = 0.60
Telle est la distance horizontale qui devrait exister dans cet exemple entre la sortie d'eau de
la tête et le premier point de la roue rencontré par la ligne d'eau
moyenne
Pour que la courbe se maintienne il faut que la charge dans le canal de tête soit
constante , ce qui oblige à commander la petite vanne en fonction du débit.
En cas de mauvais réglage et pour les faibles débits , l'eau pourrait tomber
"trop tôt" et faire tourner la roue à l'envers
Une protection couvrante évitera ce fâcheux désagrément.
2 Avec coursier
En reprenant la figure qui correspond à ce type d'admission on verra que la
pente du coursier , qui ne dépasse pas 1/10 , donne un angle non convenable car
sa valeur serait de 5.7 °
Si on veut maintenir un coursier il faut donc qu'il soit cylindrique ou même
parabolique !
3 Remarques
Cette question a échappé à bien des
roues anciennes qui étaient alimentées empiriquement , parfois avec un simple
trou dans le petit canal laissant tomber l'eau à la verticale
Solution qui avait le mérite de faire tomber l'eau en un point précis , sans
plus
Retenue de l'eau dans les augets
De plus il faut tenir compte de la possibilité pour l 'auget de garder l'eau
le plus longtemps possible ; cette possibilité est liée à la valeur de
l'angle q qui vient s'ajouter aux angles déjà vus.
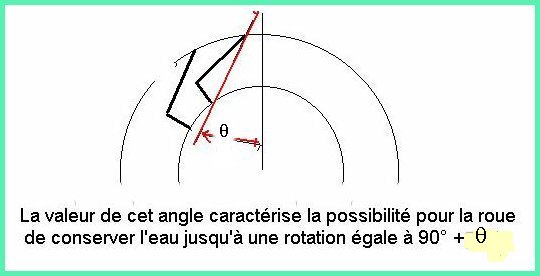
Plus cet angle est grand , plus
l'auget va pouvoir descendre en donservant son plein.
Mais il ne faut pas non plus que les "coude" des 2 parois planes crée
un obstacle au remplissage
Au delà , l'eau diminuerait de volume dans les augets
s'il n'y avait pas la présence d'un coursier inférieur de bonne fabrication
Précision du coursier , jeu aussi faible que possible , admission bien réglée
, tels sont les petits
détails qui feront la différence entre une roue soignée ou une fabrication
grossière
La différence sur le rendement peut atteindre 10 à 15 points
Notre image en haut de cette page montre un coursier médiocre ou l'eau est mal
retenue
Proportions de la roue
Le diamètre est fixé par la hauteur
de chute , donc seule la largeur et aussi la hauteur de couronne permettront
d'adapter la roue au débit
La hauteur
de la couronne ne doit pas être excessive , ce qui déplacerait
trop le centre de gravité des masses d'eau vers le centre et serait
donc la cause d'une perte de puissance excessive (voir en particulier ce
qui a été dit au sujet de la roue
parfaite )
En général un coefficient
de 0.8 environ sera adopté pour le passage du diamètre extérieur
de la roue à celui du diamètre intérieur dénommé
parfois aussi plancher : en effet dans la construction en bois on fermait
par des planches le fond des augets .
On pourra consulter une page qui traite de l'épure
des aubes mais sa rédaction devra étire revue
Logiciel de calcul
On trouvera dans le logiciel de calcul
une pagé de calcul réservée à la roue au dessus 'comme d 'ailleurs d'autres
roues)
Les paramètres internes de ce calcul sont ceux de cette page et de la page
préliminaire intitulée :
Fonctionnement
de la roue au dessus
UN PEU DE CALCULS
accessible depuis la page d'accueil
via ETUDE D UNE ROUE
Retour

 Désignons (fig.) par Vo la vitesse de l'eau qui arrive , a
l'angle de cette vitesses avec la
circonférence externe de la roue , Ve la vitesse périphérique , Vr la
vitesses relative
Désignons (fig.) par Vo la vitesse de l'eau qui arrive , a
l'angle de cette vitesses avec la
circonférence externe de la roue , Ve la vitesse périphérique , Vr la
vitesses relative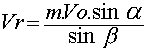
 (voir ci après)
(voir ci après)