L'eau qui court dans une rivière a une certaine énergie
Les premières roues utilisaient cette énergie , laquelle devient intéressante dans les courants rapides.

L'étude théorique ci après ne semble pas avoir été effectuée , à ma connaissance
Je serais reconnaissant à tout visiteur qui aurait des informations sur la question de me les communiquer
Aussi l'étude que je vais décrire ci après est déduite de la logique hydraulique mais j'en assume seul la responsabilité sans garantie
ANALYSE AVEC LA FORMULE DE BETZ
La puissance récupérable théorique d'une eau qui s'écoule à la vitesse de 1 m/s est de 500 watts/m2 .
En effet l'énergie cinétique par seconde de la veine d'eau est P = 1/2 * m *V^2 , m étant la masse par seconde
et comme m = r* Q
m = r* S * V
P =1/2 * r* S * V^3
avec r =1000 kg/m3 pour l'eau
P = 500 * S * V^3
Avec une hélice placée en travers du courant le résultat nous est donné par la formule de Betz ( éoliennes )
P = (8 / 27) * r * Sm
* V^3
Sm: section du moteur éolien
V vent éloigné amont
et S = 1 m2 soit un
diamètre de veine d'eau de 1.13 m.
Si on considère la veine amont :
P = (8 / 9) *
(1/2 ) * r * S
* V^3
Il faut bien noter que S et V désignent des valeurs nettement en amont de la
roue
Pour l'eau :
P = 444 * S * V^3 watts m2 m/s
c'est le max. de la puissance théorique
La section Sm balayée par la roue est plus grande que S et la vitesse dans la
roue est plus petite que V comme on le verra ci après
Compte tenu du rendement de l'hélice
(env. 0.7) la formule devient
P =310
* S
* V^3
watts m2 m/s
et si on remplace S par
p * (D^2)/4
P = 244
* D^2
* V^3
watts m2 m/s
On trouve souvent dans les études un coefficient pratique de 200 au lieu de
244
La formule n'est applicable que si :
La section est circulaire
La veine est située en plein milieu de la section droite du canal ou rivière
Les dimensions du cercle sont petites par rapport à cette section droite
Remarquons que l'eau étant un fluide incompressible , la répartition des
filets liquides sera moins rigoureuse que pour l'air .
Il faut une hélice bien tracée placée en travers du courant pour récupérer
cette puissance non pas en totalité certes , mais en partie seulement toujours à
cause du rendement qui se révèle comment ne dépassant pas 0.7
Comme on démontre que la vitesse dans la roue est les 2/3 de la vitesse
amont, le diamètre de roue serait de 1.13 * sqr(3/2) soit
1.38 m.
Si la vitesse de 1m/s est la vitesse amont , dans la roue elle est donc plus
faible et à l'aval elle n'est plus que le 1/3 de la vitesse amont
L'écoulement se rétablit ensuite à l'aval grâce à ses
dimensions supposées en fait , infinies
Finalement la puissance sur l'arbre de l'hélice sera de 311 watts avec
rendement 0.7
Avec 2m/s elle serait 8 fois plus grande : 2488 watts
D'une manière plus générale , la
puissance recueillie sur l'hélice de diamètre D sera donnée pour l'eau par la formule
approchée :
P=163 * D * D *V^3 en watts qui correspond à la formule de Betz affectée
d'un coefficient de 0.7
soit encore
P = 208 * S * V^3
watts m2
m/s
PLAQUE IMMERGEE ET POUSSEE
La
plaque est
placée perpendiculairement au courant.
L'écoulement se fait avec une énorme turbulence à l'arrière de la plaque
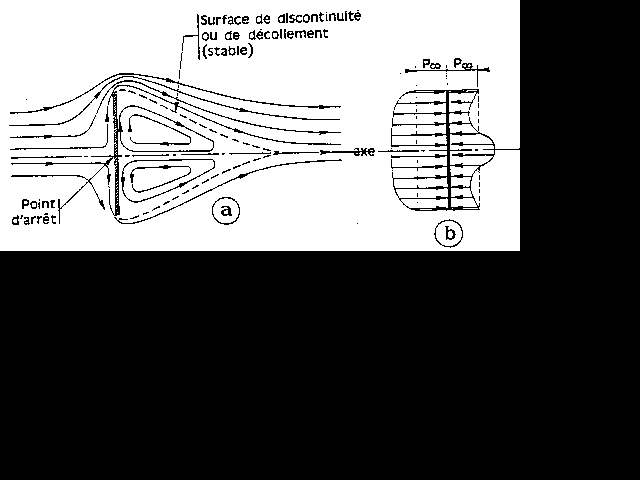
La force exercée sur cette plaque maintenue dans un premier temps immobile est
selon la formule qui s'applique aux obstacles dans les écoulements est , le
nombre de Reynolds étant inévitablement élevé :
F =1/2 *r * S * V *V *
Cx
avec r masse
spécifique de l'eau = 1000 kg/m3
F en Newtons
S en m2
V en m/s
Cx pour une plaque plane carrée =1.2 d'ou :
F =600 * S * V *V
Si la plaque recule à une vitesse v , la formule devient
F =600 * S * (V-v)^2
On peut imaginer le système mécanique suivant :
La plaque est montée sur un chariot et ce dernier roule sur des rails situées
sur les 2 rives opposées du canal
Le chariot tire un câble , lequel monte une charge le long d’un pylône par
l’intermédiaire de poulies de renvoi
Supposons H la longueur de montée qui est égale à celle de la traction.
La masse m qui doit être adaptée à la poussée a gagné une énergie égale
à mgH
et l’opération a duré un temps i
L’énergie en joules sera
W=F*H
= 600 * S * (V-v)^2 * H
Cette énergie est variable et comme dit la masse m doit être adaptée
Plus intéressante est la puissance :
P =600 * S * (V-v)^2 * H/t = 600 * S * (V-v)^2 * v
que l’on peut écrire en variables relatives avec a
=v/V
P
=600 * S * V^3 * a
* (1 - a
) ^ 2
La variable a
varie de 0 à 1
La dérivée dP/da
s’annule pour
a
=1/3 qui correspond à la puissance max
Soit
P = 90 * S * V^3
La puissance max est la suivante toujours pour 1 m2 de surface physique
| V m/s | 0.6 | 1 | 2 | |
| P watts | 19 | 90 | 720 | |
| P hélice Betz | 208 | 1664 |
On
voit l'énorme différence entre l'hélice et la plaque.
Si on admet que le rendement dans le cas de la plaque est égal à 1 , celle
ci ne récupère que 18% de l'énergie , contre 60% pour l'hélice.
LES ROUES PENDANTES

On
tombe ici dans le cas ancien des roues montées souvent sur bateaux amarrés
et qui étaient connues sous le nom de roues pendantes. ou encore roues
au fil de l'eau ;
l'avantage des bateaux était d'obtenir une régulation parfaite de
l'enfoncement de la roue quelque fut l'état de la rivière .
L'étude de ces roues a un caractère historique , voire nostalgique.
Elles devaient être montées assez haut car les pales ne doivent pas enfoncer
trop dans l’eau.
Ces roues utilisent seulement l'eau de surface sur une faible profondeur
(celle des pales) et malheureusement la vitesse en surface est plus faible
qu'en profondeur moyenne
Et les pales dans l’eau ont un effet moteur sauf pour celles qui ne
travaillent plus et jouent un rôle inverse .
Ces roues sont de construction très simple , avec souvent des pales droites
Cette roue très simple est le
type d'une roue au fil de l'eau
De plus la roue va se comporter comme un obstacle ; il y aura inévitablement
une petite remontée du niveau amont , et une grande turbulence coté aval, on
voit que le problème n'est pas simple à étudier par le calcul.
Cependant cet obstacle va augmenter la vitesse de l'eau autour de lui et c'est
ce que l'on recherche.
L 'action de l'eau sur la roue pendante a une petite ressemblance avec cette
action sur la plaque
immergée
Mais on fait certainement une erreur très importante en assimilant la roue à une pale
unique
ANALYSE ELEMENTAIRE
Nous commencerons par chercher à comprendre ce qui se passe dans une roue à 4 pales
Nous supposerons d'abord la roue enfoncée presque jusqu'au moyeu
Prenons le point gauche comme origine dees angles
CALCULS DES ACTIONS SUR UNE AUBE
Un calcul valable n'est possible que si on se place dans la condition une
seule aube active à un un instant quelconque
Les positions de l'aube seront considérées depuis le premier contact avec la
surface de l'eau et son passage à la position verticale basse
Après ce dernier passage , l'aube reçoit encore une certaine poussée que
nous négligeons en première approximation.

Une aube formant un angle a
avec le courant (en fait , il faut considérer la vitesse relative et non la
vitesse absolue) reçoit une poussée Po et une traînée Tr
avec :
Px=1/2 *r * S * V *V *
Cz
Tr =1/2 *r * S * V *V *
Cx
La force totale résultante peut s'écrire
Fa = 1/2 *r * S * V *V *
racine (Cx^2+Cz^2)
La projection de Fa sur une direction perpendiculaire à l'aube donne la force
utile Fu
Fu= Fa * cos ( b
- a
) avec b=
atn(Cx/Cz)
Connaissant Fu pour toutes les positions nous en déduirons le couple total
puis le couple moyen.
Co=(S
( Fu
* Rm
))
/ nbpositions
, Rm
étant la distance du centre de gravité de l'aube au centre de la roue
A la suite de quoi la puissance s'en déduit facilement :
P= Co * W
W
étant
la vitesse angulaire en radians/s
Le calcul ci dessus demande la connaissance de la polaire Cx,Cz pour une
plaque sensiblement carrée et pour des angles d'incidence allant de 0 à pi/2
Ce calcul par la théorie des ailes portantes demande que l'eau traverse la
roue
A suite de quoi
il peut
être assez facilement traité par ordinateur et donner un résultat
approché en se limitant à un petit nombre d'aubes .
Le calcul montre que la puissance/m2 augmente avec le nombre d'aubes , mais la
puissance effective diminue.
Cette diminution est liée à la diminution de l'enfoncement des aubes.
Il est donc intéressant d'avoir un grand diamètre car la puissance est
proportionnelle au diamètre
Quand à la vitesse de rotation , elle sera telle
que la vitesse linéaire de la circonférence soit environ le 1/3 de la vitesses de
l'eau , comme pour la plaque .
Pour en savoir un peu plus
Par ailleurs une très ancienne étude datant du 19ème siècle et qui est la
seule que j'aie trouvée sur la question donne des valeurs probablement
empiriques ou optimistes.
Voir le texte intégral - malheureusement court - de cette étude , en fin de
page
Le tableau ci dessous donne les résultats de la puissance en watts/m2
d'aube pour notre logiciel et cette ancienne roue en fonction des données de l'auteur et pour
différentes vitesses du courant.
Noter que dans le texte la puissance parait inévitablement en fonction de l'époque
évaluée en kgm/seconde , il faut multiplier par 10 pour avoir des watts.
| WATTS | V= 0.6 m/s | V=1 m/s | V=2 m/s | V=3 m/s |
| Calcul logiciel 8 aubes | 29 | 137 | 1100 | 3700 |
| Calcul logiciel 16 aubes | 38 | 179 | 1432 | 4856 |
| Etude 19ème siècle | 23 | 100 | 800 | 2700 |
.
Avec un coefficient de vitesse de 0.4 , l'étude ancienne avait
fait une bonne évaluation .
Par ailleurs la puissance y est proche de la valeur de celle
de la plaque .
Notre étude est évidemment approximative , mais les valeurs renvoyées sont
vraisemblables.
Enfin nous n'avons pas tenu compte de la largeur de la roue par rapport
à celle de la rivière , ni de la profondeur et autres paramètres.
On peut calculer la hauteur fictive de cette "chute"
Ainsi avec uns section de brassage de 1 m2 et V=1 m/s le débit est de 1 m3/s
La hauteur correspondant à une puissance de 200 w est de 0.20 m
Tout ceci évidemment en valeurs théoriques
Il est évident que la roue perturbe plus ou moins, selon les largeurs
relatives , l'écoulement de la rivière , au moins sur une certaine
longueur.
Une étude sur modèle réduit permettrait certes de démystifier le problème
s'il valait la peine d'être étudié , le calcul théorique rigoureux
étant impossible sauf par des calculs hydrodynamiques très complexes .
Extrait du Dictionnaire de l'industrie et des arts industriels Paris
1887
Roues pendantes.
Sur le bord des grands cours
d’eau, principalement de ceux dont le
courant est assez rapide, on
emploie depuis longtemps des roues à pales portées sur des
bateaux, ou
roues pendantes leur diamètre ne dépasse pas 4
à 5 mètres, et leur
longueur, 2 à 5 mètres. Les palettes
ont de 1/5 à 1/4 du rayon de la roue, et leur
écartement
sur la circonférence extérieure
est égal à leur hauteur. A leur
passage dans le plan vertical, leur
bord intérieur enfonce dans
l’eau de 5 à 20 centimètres;
il convient de les incliner sur le rayon,du
côté amont, sous un angle
d’environ 30°
Si le courant est profond, on
pousse l’ immersion jusqu’à
50 centimètres; mais
on réduit l’inclinaison à 15°
. La vitesse de la circonférence décrite par le centre de gravité des aubes
est réglée à 0,4 de la
vitesse du courant; le travail
par seconde peut être évalué à 20 fois le produit de la
surface de l’aube par le cube de la vitesse du courant.
Cependant , d'autres documents plus dignes de foi donnent un
coefficient de 10 au lieu de 20.
C'est cette dernière valeurs que j'ai retenue.
Il faut encore tenir compte du fait que la partie de l'aube qui est dans le
sillage de celle qui la suit doit être déduite de sa hauteur , ceci étant
valable surtout pour les aubes qui arrivent à la partie inférieure.
L'examen de la turbulence autour d'une plaque nous a d'ailleurs montré comme
les lignes de courant sont perturbées autour de la plaque.
Si les aubes sont inclinées vers l'avant , cet effet peut être presque
annulé sauf pour les 2 ou 3 dernières.
Connaissant Fu pour toutes les aubes nous en déduirons le couple total
Co=S
( Fu
* Rm
) Rm
étant la distance du centre de gravité de l'aube au centre de la roue
A la suite de quoi la puissance s'en déduit facilement :
P= Co * W
W
étant
la vitesse angulaire en radians/s
ET DU NOUVEAU POUR
CES ANCIENNES ROUES
Retour page
d'accueil