La vitesse absolue n'est plus que la vitesse d'entraînement
Nous allons voir ces points plus en détail
Le coursier
Les inventeurs ont commencé par des coursiers rectilignes , ces derniers ayant une inclinaison de 6° environ
Par la suite on a construit des coursiers circulaires puis en développante de cercle , ces derniers avaient quelques avantages mais li n'est pas primordial d'entrer dans ces détails.
Le coursier s'arrête à la verticale du centre afin que l'eau puisse retomber
Cette condition est importante.
Introduction du jet
Avec un angle de 30 ° comme vu ci dessus l'angle entre la vitesse de l'eau et la circonférence a sensiblement la valeur moitié , soit 15 °
Pour l'examen des triangles des vitesses , nous considérons 3 notations et 3 points
notation V pour la vitesse absolue
notation W pour la vitesse relative
notation U pour la vitesse d'entraînement
Indice 0 pour l'entrée
Indice 1 pour la "sortie" ou plus tôt la remontée de l'eau dans le haut de l'aube
Indice 2 pour la sortie finale
Trajet initial du fluide
En examinant le figure (disponible sous qq jours) on voit que l'eau entre tangentiellement à l 'aube dans laquelle la vitesses est W0 dont la grandeur est sensiblement V0/2 , ce qui est aussi la valeur de U0
Mais cette vitesse va rapidement diminuer sous l'effet de la pesanteur , l'aube étant alors dans la zone de la verticale.
Notons cependant que l'aube doit être emprisonnée sur 2 ou 3 pas pour permettre cette remontée qui est moins rapide que la rotation
La hauteur de remontée correspond à l'équation de Bernoulli par rapport à un référentiel lié à la roue
Cette hauteur a pour valeur W0^2/( 2* g) ou encore V0^2/ ( 8 * g)
Le point correspondant est le centre de gravité de la masse d'eau qui a remonté, la vitesses absolue de cette masse reste la vitesses d'entraînement en ce point
Nous n'avons que cette méthode pour évaluer le rendement car les équation d'Euler sont inapplicables , l'eau ne quittant pas la surface
Cette méthode nous permet de calculer l'énergie restante en ce point : c'est moins du 1/4 de l'énergie initiale
Sortie de l'eau
Le triangle des vitesse à la sortie est quasi inutile car il est clair et contrairement à une opinion répandue autre fois , que l'eau n'agit plus positivement sur l'aube dans sa descente , car elle part d'une vitesses relative nulle, ne colle plus aux parois et se trouve dans une zone tourbillonnaire.
D'après ce triangle , Certains auteurs anciens ont constaté que la vitesse absolue V2 était très faible , son carré est alors quasi nul ; le rendement calculé étant alors de 93 % !
Ce raisonnement est en fait l'application à la totalité du trajet du Théorème d'Euler , ce qui est interdit puisque le bord d'entrée et celui de sortie sont confondus
Rendement de la roue
C'est le premier trajet de l'eau qui donne la puissance
Le rendement calculé est élevé , plus de 80%
Pour une roue très soignée et bien établie , cette valeur est au moins de 10 points plus faible
Mais cette roue reste assez remarquable
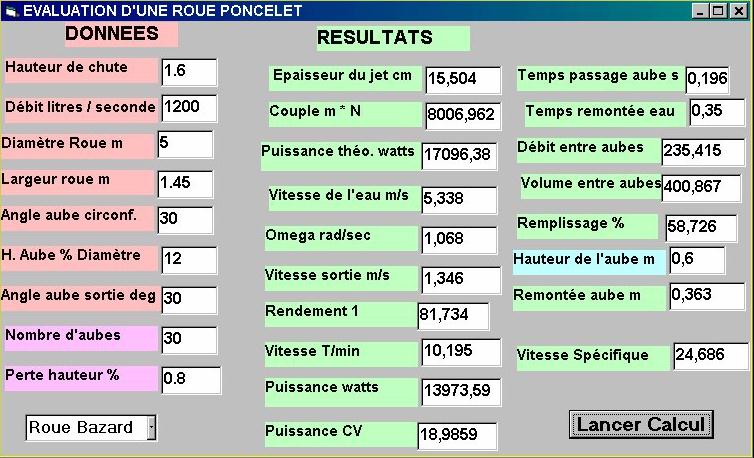
Le calcul présenté est celui d'une roue proposée Dans l'ouvrage de Monsieur BAZARD (Cours de mécanique Hydraulique Albin Michel 1918 )