Les Roues en dessous

(Voir aussi la roue pendante)
En utilisant l'énergie cinétique d'une lame d'eau passant sous une vanne réglable , nous utilisons toute l'énergie cinétique de la chute si la vanne commande la totalité de la hauteur de cette chute.
Cette vanne nécessite une construction robuste adaptée à la pression de l'eau à sa partie basse .
Le plus souvent on opte pour la solution d'une vanne inclinée vers l'amont ce qui permet de rapprocher la roue de la vanne et donc de la lame d'eau.
La lame se trouve au point bas , à un niveau un peu supérieur  à  celui du canal de fuite compte tenu de la nécessité d'un coursier incliné pour éviter la formation d'un ressaut avant que la lame rencontre les pales.

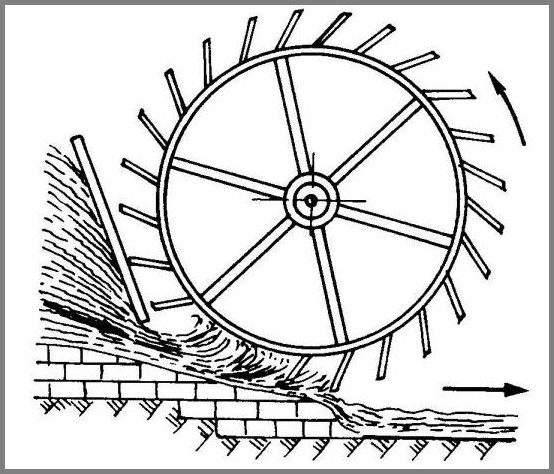
Le réglage de la lame et donc du débit se fait par la vanne
L'énergie de la lame d'eau sera uniquement sous forme cinétique
la vitesse de l'eau étant V1 = racine(2gH)
On prend pour la vitesse périphérique der la roue la moitié de cette valeur
La roue ne comporte plus d'augets , mais des pales planes ou légèrement courbées .
La construction est donc relativement simple comme le montre cette représentation ancienne.
Triangles des vitesses

A l'entrée , le jet est sensiblement perpendiculaire à la pale au bas de la roue (le dessin étant un peu différent mais cela change peu de choses)
Le triangle se réduit à 3 vecteurs colinéaires qui sont
 V1 , U1 = V1/2  W1 =U1/2
A la sortie le triangle est rectangle isocèle
U2=U1= V1/2
W2= V1/2
Il en résulte que 
V2 = V1/racine(2)
L'énergie perdue à la sortie est V2^2/(2g) soit V1^2/2*(2g)
C'est la moitié de l'énergie de la chute
 La valeur théorique maximale est de 50% et les plaques courbes n'améliorent que peu ce rendement
Le rendement réel est encore plus médiocre et  souvent inférieur à 30% .

Les causeu en sont : 
L'eau s'évacue mal des pales , il y engorgement ce qui n'est pas le cas   pour une plaque isolée et libre .
La roue barbote dans le canal de fuite , là ou l'eau a déjà une moindre vitesse ; il en résulte un freinage supplémentaire .
Le choc de la ligne de courant moyenne se fait à une certaine distance de la circonférence externe , là ou l'action serait la plus efficace afin d'avoir le meilleur couple . Pour cette raison , on augmente le diamètre de la roue qui peut souvent atteindre le double de la hauteur de chute.

La vanne est généralement suivie d'un coursier plus ou moins incliné

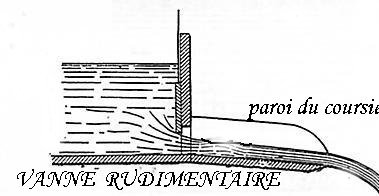
La charge d'eau est la différence de  hauteur entre le niveau amont et une  ligne de courant supérieure du jet juste à la sortie
Cette charge en m est égale à V2^2 /(2g) = y1-y2 sur le dessin

L'exemple ci dessous donne pour une vanne droite non biseautée 
et une largeur de canal de  0.50 m, les débits correspondants
Le coefficient de contraction (rapport entre la hauteur de la lame d'eau et l'ouverture) est de 0.6 environ

C'est le rapport entre y2 et h (ne pas se fier au dessin)

Nous verrons que la vanne peut bien sur être droite ou inclinée

Calcul d'une roue en dessous 

Comme précédemment nous allons raisonner sur un exemple et prendre cette fois une chute d'eau moitié de celle de  la roue en dessus mais avec le même débit
Ainsi la puissance théorique de la chute sera moitié de celle calculée pour la roue en dessus

La lame d'eau
Au débit maximum (360 litres/seconde) la vanne devra être levée de 0.062 m  pour une largeur de 1.20 mètres comme précédemment.
Dans la formule nous prendrons h=2.60 - 0.03 = 2.57
Q=3 * 0.0744 *racine (h)= 0.357 m3/s
La vitesse est racine(2gh) = 7.1  m/s
La section du jet est Q/V=0.0503  m2

Sa hauteur Hjet est  de 4.19 cm

La puissance mécanique du jet est 9082 watts ce qui à peu de chose près correspond à notre point de départ , la différence s'expliquant par l'approximation inévitable sur la valeur du coefficient de contraction de la lame d'eau  sous la vanne
Le diamètre de la roue doit satisfaire à l'obligation d'une vitesse circonférentielle  égale à V/2 soit 3.55 m/sec.
En prenant D=4 m la vitesse sera N=17 t/min ce qui est une vitesse rapide pour une roue .

Le nombre de pales doit être suffisant pour que le jet soit toujours en contact avec au moins une pale
Pour ce faire il faut que lorsqu'une pale quitte le jet une autre prenne sa place à l'endroit ou la  première avait commencé à le toucher.
La figure ci contre qui n'est pas à l'échelle montre que l'angle a entre 2 pales successives doit être tel que
cos(a) = 1- 2*Hjet /D

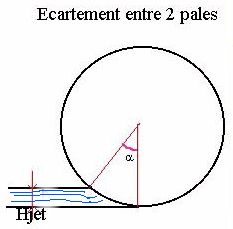
Dans notre cas on vérifie facilement que a est égal à un peu plus de 11 degrés.

En prenant 12 degrés nous aurons 30 pales sur la roue comme valeur minimale
Les pales seront droites ou légèrement courbées.

La hauteur des pales est empirique : il faut laisser à l'eau assez de surface pour qu'elle puisse exercer son action d'autant plus que cette action est empêchée sur les cotés par les bajoyers.

Théoriquement la pale devrait toujours rencontrer l'eau à la verticale
Dans certaines roues (type PONCELET) on a imaginé de faire remonter l'eau dans la roue pour récupérer une partie de l'énergie perdue 

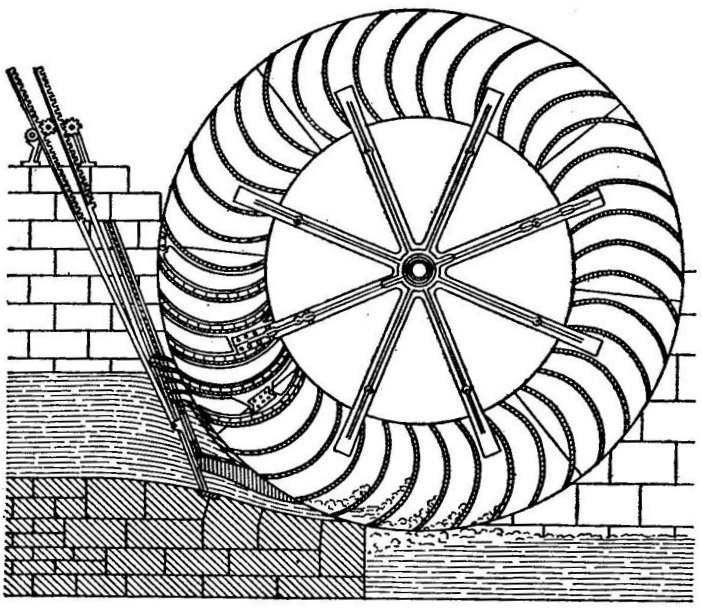
Le fonctionnement de la roue PONCELET est en fait largement empirique .

On verra ci contre la reproduction d'une roue PONCELET dont le vannage est assez complexe 

On trouvera dans l'histoire des roues une autre représentation de ce type de roue .

Une étude plus précise de cette roue PONCELET  se trouve dans le site .

D'une manière générale une machine est d'autant plus satisfaisante qu'elle procure le plus grand service tout en ayant le plus faible encombrement possible. Le poids et le prix en dépendent.


Une roue encore plus rustique est la roue au fil de l'eau ou roue pendante qui sera examinée sur une autre page

Retour page d'accueil