Etude technique

LA ROUE A AUBES
DU MOULIN DE LUTTERBACH 

La roue rénovée en Octobre 2000



Ce moulin appartenait encore récemment à la savonnerie de Lutterbach (Haut Rhin)

Son origine remonte au 15ème siècle



La roue a été démontée en 1998 en vue d'une réfection et dans les cadre des travaux entrepris par le Syndicat de communes de l'agglomération de Mulhouse pour transformer ce moulin en centre d'initiation à la nature pour les jeunes des environs .


Donc , L'heure approche ou la roue tournera à nouveau

pour l'étude générale de ces machines voir
   toutes roues

LE DEBIT INSTALLE
Les débits ont été calculés par la formule classique de l’écoulement sous une vanne verticale.
On verra ci-après sur le Tableau des débits qu’avec les dimensions du canal d’amenée de l’eau à la roue, (largeur 1.50 m , profondeur 0.67 m.) le débit optimal se situait sensiblement vers 1 m3/sec.
On suppose par la suite que le hauteur d’eau dans le canal se maintient à 0.60 m.
On verra aussi qu’il y a une valeur optimale pour la hauteur de levée de la vanne qui alimente la roue .
Cette hauteur se situe vers 0.40m. ; si on continue à lever, la puissance n’augmente plus et finit par diminuer.
Si la vanne est complément levée, le calcul est celui d’un « déversoir dénoyé à débit maximum indépendant du niveau aval » (ESCANDE, Hydraulique générale, tome 2).Le calcul donne alors 1.19 m3/sec. pour le débit ; la hauteur de l’eau dans le canal est réduite à 0.40 suite à une rupture de pente , conséquence du passage d’un écoulement laminaire à un écoulement torrentiel.
On suppose bien entendu dans tous les cas que la rivière peut assurer le débit.
La section du canal étant de 0.9 m2, la vitesse de l’eau est de 1.1 m/sec si le niveau maximum est maintenu.
Cette valeur est bonne car ne conduisant qu’à une faible perte de charge dans ce même canal.

LA PUISSANCE HYDRAULIQUE
La hauteur de chute ayant été mesurée comme sensiblement égale à 2 mètres, la puissance hydraulique théorique c’est à dire avec un rendement qui serait de 100 % est de :
9.81 x 1 x 2 = 19.2 Kw
correspondant à 26 CV
Nous allons voir qu’une petite partie seulement de cette puissance était récupérée par la roue.


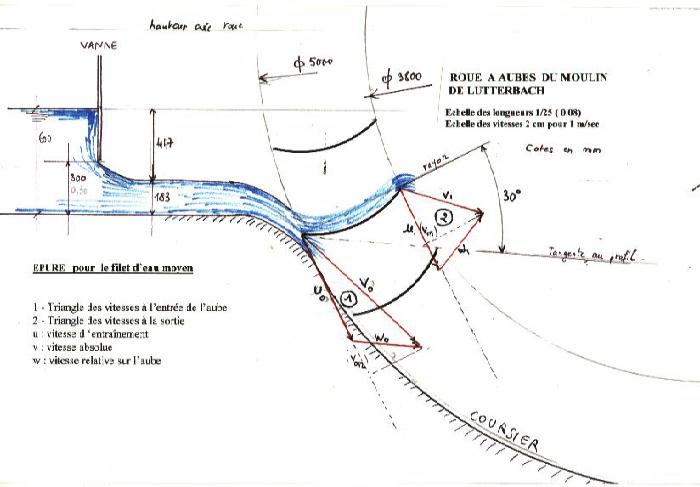
LA ROUE
D’un diamètre de 5 m elle comporte 30 palettes (ou aubes) courbes ; l’espacement périphérique entre palettes est de 52 cm.
La largeur des palettes est celle du canal et de la vanne : 1.50 m.
Le développement des palettes est sensiblement de 0.65 m.
La géométrie de la roue est celle d’une roue Poncelet , mais son installation ne correspond nullement  à cette roue .
Certains l'ont assimilée à une roue de poitrine , ce qui est faux vu l'absence de fonçure.
La roue Poncelet avait un assez bon rendement pratique (0.6) ; mais cette roue était attaquée convenablement c’est à dire à la partie inférieure, ce type de roue n’utilisant que l’énergie cinétique de l’eau et non celle de gravité , ce qui n’est pas le cas au moulin de Lutterbach où l’attaque de l’eau se fait beaucoup plus haut.

Il en résulte de graves erreurs de principe qui conduisent à un rendement faible .

L ‘ECOULEMENT DE L‘ EAU
Nous pouvons examiner dans le Tableau des débits la vitesse de l’eau à la sortie de la vanne.
Avant de rencontrer les aubes l’eau court encore sur un petit déversoir bien profilé ; il augmente un peu la vitesses de l’eau ; la hauteur supplémentaire est d’environ 0.30 m.
On tient compte de cette dénivellation pour calculer la véritable vitesse d’attaque ; Cette valeur est indiquée dans le tableau sous « V Entrée aube ».
Pour une levée de 0.30 m., cette vitesse (3.75 m/sec) correspond à 35 % de la puissance totale.   
                        
                                                     L' image montre la disposition  adoptée  pour l'arrivée de l'eau sur la roue

La puissance indiquée dans la colonne puissance tient compte de cette énorme réduction.
Si la roue tourne à une vitesse convenable, le triangle des vitesses à l’entrée sur l’aube est très correct ; autrement dit la vitesse relative de l’eau sur la palette a la même direction que le profil a son entrée ; donc absence de choc ce qui est primordial. (1)
En s’aidant de la géométrie de la roue on peut reconstituer assez bien le triangle idéal pour une vitesses de l’eau donnée, et compte tenu de la direction de la vitesse de l’eau juste avant l’entrée sur l’aube.
Voir l’épure annexe tracée à l’échelle de 1/12.5 pour la ligne d’eau moyenne et une levée de 0.30 m.
Cette dernière étude montre que la vitesse de la roue était de 8 à 10 tours /minute.
Le triangle des vitesses à la sortie nous montre que l'eau est éjectée vers l'intérieur de la roue avec une vitesse absolue qui graphiquement est environ les 2/3 de la vitesse d'entrée.
Cette éjection tient a l'absence de fonçure.
On pourrait craindre que la remontée géométrique de l'eau ne soit encore cause d'une perte supplémentaire.
Fort heureusement , la vitesse relative sur l'aube (env. 1.5 m/s ) est telle que la roue a tourné de 2 à 3 aubes environ quand se produit la sortie et de plus il y a une action de gravité sur 2 à 3  aubes au maximum.
Malheureusement cette action se produit alors que le bras de levier n'est pas optimal .
Enfin on peut estimer à 0.30 la hauteur ainsi récupérée.
Par la suite il n'y a plus d'eau dans les aubes.
Le coursier est devenu inutile .D'ailleurs le jeu considérable entre la roue et les bajoyers interdirait  lui aussi la conservation de la masse d'eau
 On pourrait en déduire donc  que le reste de l'énergie cinétique est perdue.
Cependant on peut se poser une question : L'eau éjectée ne va t elle pas retomber sur les aubes inférieures et donner un surcroît de puissance comme dans une roue Banki ?
La réponse n'est pas facile ; il faudrait pouvoir faire une épure précise des aubes et vérifier que l'eau peut retomber (en jet parabolique) sur une face convenable de l'aube et avec un angle convenable ; ces conditions ne sont pas faciles à remplir ; de plus elles supposent un maintien rigoureux de la vitesse de tracé , conditions draconiennes pour l'exploitation d'un moulin.
Enfin si k'eau tombe sur le dos de l'aube le couple sera négatif entraînant une perte de puissance
On reste donc dans le doute : roue partiellement ratée ou roue de génie ?

Et dans le doute nous laisserons de coté cette puissance supplémentaire qui aurait fait de cette roue une merveille.

Un complément de réponse se trouve dans la note technique   à ignorer pour ceux qui ne veulent pas se casser la tête dans les calculs

On évaluera les hauteurs 'turbinées" grossièrement comme suit en totalisant les 2 phases successives ::
Pour la partie vitesse » : 0.75 m
Pour la partie gravité :  0.25 m
Soit au total une  hauteur  de 1 m
Le rendement (théorique) est de 1 / 2 soit 0.5 et le rendement réel est à affecter d'un coefficient de 0.7 environ d'ou un rendement global de 0.35
Et une puissance sur l’arbre de 26 x 0.35 = 9 CV soit 6.6 Kw environ 
avec une vitesse de rotation de 8 à 10 T/min.
Les valeurs du tableau ci dessous , effectuées avant la retouche des calculs , sont à peine inférieures.

TABLEAU DES DEBITS , VITESSES , PUISSANCES



(1) Il ne faut pas croire selon une idée assez intuitive, mais fausse, que des palettes plates attaquées par un jet d’eau perpendiculaire donnent un bon rendement ; au contraire il y a une forte turbulence du fait du choc et qui dit turbulence dit dégradation d’énergie.
Voir le formulaire

Il faut tout de même remarquer la roue inventée vers 1824 par Poncelet ,mathématicien et ingénieur remarquable , roue  assez empirique et intuitive ,   était un énorme progrès.