TOURNIQUET
On trouve dans de vieux laboratoires
de physique des appareils du genre représenté par l'image

Cet appareil est formé d'un vase piriforme tenu, par une potence de bois, ce
qui lui permet de tourner autour de son axe vertical, au dessus d'un bassin métallique.
Le vase porte à sa partie inférieure deux tubes ouverts, perpendiculaires à
l'axe de rotation, et recourbés à angles droits contraires vers leurs extrémités
Pour faire fonctionner l'appareil, on remplit le vase d'eau. La pression
latérale exercée aux extrémités des tubes, là où l'eau s'échappe, il y a
mouvement imprimé aux tubes dans une direction contraire à celle de
l'écoulement. Il en résulte un mouvement circulaire d'autant plus rapide que
les ouvertures sont plus grandes et le niveau dans le vase plus élevé. la
poussée latérale estt utilisée comme force motrice dans les roues
hydrauliques à réactions, dites turbines.
voir : http://www.inrp.fr/she/instruments/instr_hydros_tourniquet.htm
REMARQUONS l'ingéniosité du système : les tubes sont longs
et l'eau en amont est concentrée sur un faible diamètre , ce qui
favorise le fonctionnrement
Autre étude trouvée sur le web
Théorie
(simplifiée)
Soit D, le débit massique qui sort d’un tube,
ve
la vitesse d’écoulement (par rapport au tube),
On pourrait admettre comme pour une fusée, que la poussée pour un
tube est Dve et le
moment de cette poussée, par rapport à l’axe est
rDve,
la distance du jet à l’axe étant r.
Le réservoir est donc soumis au couple: 2rDve
(deux tubes).
Théorie
(plus exacte)
Soit w
la vitesse de rotation, I le moment d’inertie par rapport à l’axe, I w
le moment cinétique. Pendant la durée infinitésimale
dt l’accroissement du
moment cinétique à deux causes :
·
l’action d’un couple appliqué
Ca qui
produit l’accroissement Cadt.
Le couple Ca peut être le couple de frottement. Nous le
supposerons négligeable (Ca=0).
·
la perte de moment cinétique due à l’écoulement: la masse dm
= Ddt emporte la quantité de
mouvement vdm
= dm (wr
+ve ) = D(wr
+ve )dt
(ve est la vitesse
relative au tube et wr
la vitesse d’entraînement).
A cette perte de quantité de mouvement correspond, pour les deux
tubes, l’accroissement de moment cinétique: - 2rvdm
= - 2r D (wr
+ve )dt.
On a donc:
d(Iw)
= Idw
+ wdI
= Ca dt - 2rD(wr
+ve)dt
Calculons
dI : la modification subie est la disparition d’une couche dz,
de masse dm = Ddt,
à la surface libre du liquide dans le vase. Ce petit disque a pour moment
d’inertie
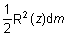 , si R(z)
est le rayon à la hauteur z.
, si R(z)
est le rayon à la hauteur z.
 .
.
En
reportant dI dans l’équation précédente, il vient :
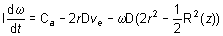
Pour
w
= 0 et Ca négligeable,
on retrouve :
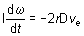
Ces analyses demandent un peu de réflexion!
par ailleurs on peut affirmer que le rendement
théorique du tourniquet fonctionnant en turbine ne peut etre > 0.5
A suivre....
ci dessous mon ancienne étude
Pour tenter de démystifier le problème nous considérerons un tourniquet
simple
J'ai fabriqué un petit tourniquet pour aider la construction de cette page
Il est facile à construire avec du tube cuivre et des accessoires pour tube à
souder à l'étain
Il comporte 2 coudes à 90° alimentés en eau par une tubulure centrale qui est
en même temps la partie tournante.
le diamètre intérieur des coudes d'éjection est de 12 mm
Il est équipé dans ma réalisation d'un manomètre 0-4 bars , un robinet
ordinaire situé en amont sert à régler la pression qui sera toujours
maintenue à 1 bar par exemple .
Pour une tubulure sans pertes de charge le débit serait de 1.6 m/s et la puissance
mécanique du jet libre de 160 watts .
Du fait des pertes de charge dans les coudes notamment elle est réduite à 120
watts environ
Le but de l'expérience est de voir ce qui se passe pour le tourniquet :
bloqué
en arrêt
libre de tourner à
sa vitesse maximale
tournant à vitesse moyenne donc fournissant de l'énergie .
Qui a compris le moulinet a compris la turbine .
La mise au point de cette expérience est passionnante
A l'arrêt (forcé) l'eau sort à la vitesse
d'éjection et exerce sur le coude un effort qui sera calculé comme expliqué
ci dessous.
A la vitesse libre , donc sans frein , le tourniquet atteint une vitesse presque
égale à la vitesse d'éjection et telle que l'eau tombe verticalement au sol .
A ce moment là , la vitesse linéaire de rotation est donc la vitesse
d'éjection un peu moins cependant à cause des pertes par
frottement
Si on veut utiliser l'énergie , il faut freiner le mouvement
Le maximum d'énergie est récupéré quand la vitesse est moitié de la
précédente.
En fait , il faut tenir compte de la perte de
charge dans le coude qui est loin d'être nulle si le coude est trop
serré
Le calcul donne les résultats reproduits sur le diagramme ci
dessous
Pour ce calcul , le coefficient de perte de charge dans le coude a été
estimé à 0.3
La Puissance mise en jeu au maximum est de 60 watts environ soit la
moitié de la puissance du jet
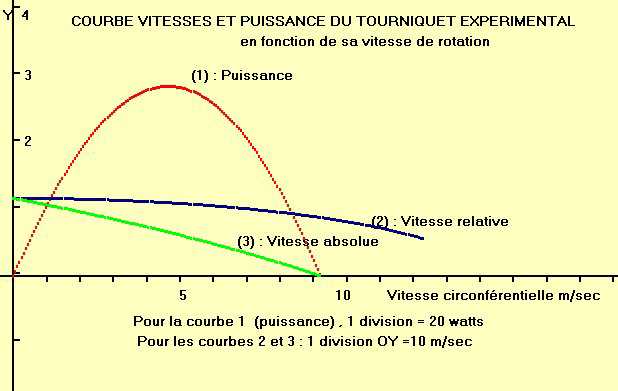
La vitesse relative est en fait la vitesse de l'eau dans une tubulure de sortie
La vitesse absolue est la vitesse de l'eau par rapport au sol
On voit que cette vitesse est nulle pour la vitesse maximum dite aussi vitesse
d'emballement
Le mystère du moulinet est de transformer "de la pression en
énergie" , ce dont les roues de moulin étaient incapables.
Le moulinet est une machine à réaction.
Nous pouvons appliquer l'équation d'Euler à
cette machine si le coude n'est pas un coude brutal
Heff = (U0 * V0N - U1 * V1n) / g
U0 est très petite et de toute façon V0n est nul
U1 , V1 , sont colinéaires alors les Vn sont égaux aux V
D'ailleurs la vitesse de l'eau dans le tube est constant en grandeur et de
valeur V1 en sortie
La vitesse absolue de l'eau en sortie est V =U1 + V1 mais vu les sens V = U1 -
V1
car V1 et U sont de
signes opposés car le tourniquet tourne en sens inverse du jet
V1 = U1 - V = V1n
Le produit selon Euler donne
g * Heff = U1 * (U1 - V) = U1^2 - V*U1
dont la dérivée par rapport à U1 est 2 *U1 - V
Elle s'annule pour U1 = V/ 2 et la
fonction passe par un maximum
Si V1 = 0 alors U1 = -W1 (Heff =0 , énergie nulle , emballement)
Rappels
Vitesse d'éjection :
Notion déjà vue
Si le pression avant la sortie est 1 bar soit 10.33 mètres d'eau , la vitesse
est racine(2 * 9.81 * 10.33)=14 m/sec
Calcul de la force s'exerçant sur un coude immobile
F = 0.707 * Q * V pour un coude à 90°
F en Newtons
Q en litres / seconde
V en m/seconde
Exemple
Q = 350
V = 4.7
F = 115 N
Je rappelle aussi que les premiers inventeurs ont essayé
le tourniquet comme turbine , ce qui a été abandonné à cause des faibles
puissances utilisables avec ce système
Retour page
d'accueil

