TURBINES A REACTION

J'ai essayé de résumer ici la théorie des machines à réaction
En général les développements que l'on trouve dans de rares ouvrages spécialisés sont longs et souvent presque inaccessibles

Je me suis efforcé de simplifier la question moyennant un minimum de  petits calculs

Nous avons déjà vu que la turbine Francis tient un rôle important dans la gamme des turbines actuelles
Cette roue a supplanté notamment les roues de type Fontaine et Fourneyron , qui pour leur époque étaient des merveilles mais dont la construction était difficile en particulier pour la Fourneyron dont le poids de la roue , mal suspendue reposait sur une crapaudine noyée
De plus le rendement de ces machine était insuffisant
En particulier dans le cas de la Fourneyron l'eau était éjectée en pure perte et la roue ne pouvait convenir que pour les hautes chutes , à cause du rendement ,mais on lui préféra rapidement la Pelton .
On aurait voulu aussi construire une roue centripète mais la difficulté était d'évacuer l'eau au centre de la machine , pour ne plus avoir les inconvénients de la machine centrifuge
Cette question fur résolue par les américains.

Ils  développaient en effet une roue toute nouvelle  qui permettait à l'eau d'avoir un parcours d'abord radial centripète puis axial.
Il fallait un tracé hélicoïdal
Ce tracé est complexe . Beaucoup de roues furent ratées , aussi bien aux USA qu'en Europe ou cette turbine , connue sous le nom de Francis du nom de son inventeur final , était souvent plus réussie avec la chance ou le flair de modeleurs que par le calcul strict .
Aussi les constructeurs se lancèrent ils dans les modèles réduits
La difficulté du calcul ne venait pas de la théorie elle même , bien maîtrisée , mais de la difficulté de raccorder entre elles un certain nombre de turbines élémentaires découpées par la pensée dans la roue principale .
Il y a en effet une grande différence dans le trajet des filets liquides entre le plafond et la ceinture de la roue
De la difficulté de relier entre eux ces différents trajets par un dessin correct de la surface hélicoïdale venait le problème (voir figure dans une autre page)

Ne pas s'aventurer dans la construction d'une Francis !!

Que le bon bricoleur ne se lance pas dans une telle aventure : le risque d'échec total est très grand 
Alors que la Pelton , même avec des augets plutôt médiocres , la Banki ,l'hélice (à condition pour cette dernière et si on n'a pas de pales orientables  , de pouvoir à posteriori et peut être dans des proportions non négligeables modifier la vitesse optimale de rotation , ce qui suppose que l'on pusse faire des essais avec un génératrice provisoire , au besoin auto excitable , attention aux surtensions !) ne sont pas tout à fait en dehors des possibilités de l'amateur , la Francis en est tout à fait .

Mais qu'est ce qu'une roue à réaction ?
Dans une Pelton par exemple la vitesse d'admission de l'eau (jet) est de 0.99 environ de racine (2gH)
La pression dans le jet est nulle , il n'y a aucune réaction.
Dans une roue à réaction , la direction de l'eau est d'abord réglée par une couronne de directrices mobiles
qui peuvent régler l'admission de l'eau de la fermeture à la pleine ouverture sans créer de perte de charge sensible
Cette couronne se situe juste à l'extérieur du cercle extérieur de la roue et très près

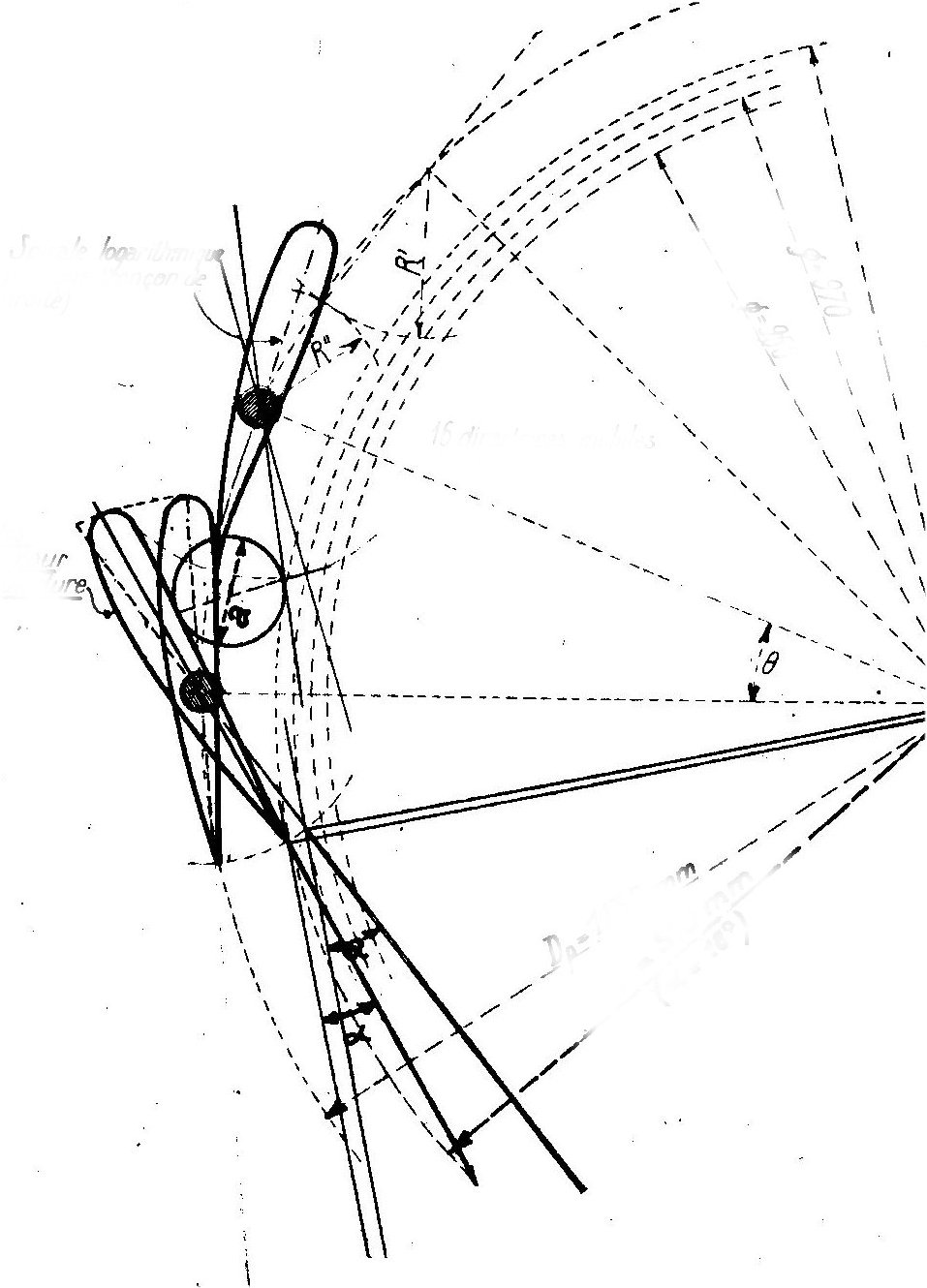
En régime de charge optimal , la direction de l'eau avec la circonférence de la roue fait un angle a que l'on voit sur la figure
Cet angle désigné par Alpha0 ( a0) dans les calculs qui vont suivre est un élément essentiel du triangle des vitesses à l'entrée de la roue mobile
L'eau a une certaine vitesse : moindre que dans la Pelton ; de l'ordre de 0.6 racine (2gH)
Cependant avec la valeur de 0.6 l'énergie de vitesse est de 36% de l'énergie totale , 64% subsistent en énergie de pression .
Le degré de réaction est ici de 0.64 (en négligeant l'influence faible de la vitesse de sortie)

Dans la roue l'eau va perdre sa pression avec un tracé d'aube tel que la vitesse de sortie soit faible


Comment l'eau cède t elle son énergie ?

Il faut raisonner sur un exemple simple

L'exemple que nous allons donner est correct dans son calcul , mais il s'agit d ' une turbine centripète cylindrique , autrement dit une turbine ou l'eau sortira difficilement de la partie centrale , autrement dit il y aura une sorte d'engorgement qui va créer une perte de charge , laquelle va se retrancher de la hauteur de chute.
Pour restreindre cet engorgement du à la rencontre intempestive de filets liquides venant de toutes directions
nous disposerons un plafonnage en entonnoir renversé.


Notre modèle ne sera donc pas utilement réalisable , car une turbine de mauvais rendement ou de volume spécifique excessif n'est plus acceptable de nos jours.
Tout au plus aurait il un caractère expérimental.
Donnons seulement les éléments simplifiés du calcul pour la partie ou l ' écoulement est théoriquement correct (distributeur et roue)
Données de départ
On peut se fixer Hauteur et débit , mais comme c'est la géométrie de la roue qui nous intéresse , et non ses dimensions ( voir similitude) , nous laisserons de coté ces grandeurs pour calculer en valeurs relatives.
Ainsi les coefficients k0, .... seront définis par :
V0 = k0 * racine(2gH)      Vitesse d'admission        
        U0 = x0 * racine(2gH)  Vitesse circonférentielle
        W0 = l0 * racine(2gH)   Vitesse relative

et de même avec l(indice 1 pour les valeurs de sortie
Le triangle des vitesses à l'entrée est facile à construire
Pour construire celui de la sortie , et le placer convenablement sur l'épure il faut étudier la question du Rendement manométrique

Ce rendement est celui de l'aube elle même , il ne concerne pas les pertes volumétriques ni celles du distributeur ni de l'aspirateur ou autres
Ce rendement correspond à une aube convenablement tracée , changements de courbures faibles , finesse et poli de la paroi, et évidemment respect des triangles des vitesses
La difficulté est de placer sur le cercle intérieur de la roue le triangle de sortie , il faut que l'aube soit bien tangente aux vitesses relatives et de plus elle doit se placer pour que sa courbure puisse être régulière

Compte tenu de l'expérience acquise sur les turbines réalisées on peut prendre une valeur de 0.89 pour ce rendement
Rappelons la formule d'Euler vue à la page Formules diverses

Heff = (U0 * V0n - U1 * V1n) / g  

avec 
V0n = V0 * cos(a0 ) composante normale de V0
V1n =V1 * cos ( a1 )              
En remplaçant facilement V0, V1, U0, U1 par le second membre des équations vues plus haut :

Heff / H = 2 *(K0 * x0  * cos (a0) - K1 * x1  * cos (a1))

C'est le rendement manométrique d'Euler

Notre logiciel a reçu une procédure supplémentaire pour résoudre cette équation , qui autrement doit être résolue par approximations , de façon que l'angle a1 soit convenable ce qui permet de connaître et de dessiner à part le second triangle
La routine calcule aussi en même temps l1 
Il faut ensuite le reporter sur l'épure de manière à respecter au mieux les conditions ci dessus
C'est le point le plus difficile car il faut que les calculs aboutissent à une aube réalisable

On pourra remarquer que le placement du second triangle des vitesses conduit à de nombreuses solutions mais si on prend un cercle pour le tracé de l'aube et si on impose à ce cercle d'être tangent aux vecteurs vitesse relative en entrée comme en sortie il n'y a qu'une solution

La feuille de calcul donne les résultats de notre exemple 

On peut modifier ces valeurs .
Il faut estimer une valeur (faible) pour K1
 et Lambda1 ( ou l1 ) est un résultat et non une donnée

On trouve dans les résultat les 6 angles et la confirmation du rendement manométrique
Cependant il faudra vérifier que le tracé est réalisable

Nous passons sous silence de nombreux points de détail
Le nombre d 'aubes varie de toute façon entre 12 et 15 en général
Trop d'aubes introduit du frottement
Pas assez n'assure pas un guidage suffisant des filets liquides

On remarque que l'angle b1 est un peu supérieur à 90° , ce qui correspond à une composante rotationnelle de l'eau en sortie et de sens inverse au sens de rotation
Tel est le développement qui devrait être appliqué à chacune des 5 ou 6 (ou plus) turbines élémentaires obtenus par des "coupes" dans la vraie Francis
Pour chaque élément les triangles seront différents
Le rendement réel est évidemment plus faible que le rendement manométrique moyen
Pour une vraie Francis , il était  de l'ordre de 86 % vers 1950 ; il atteint 95 % actuellement avec évidemment un rendement manométrique très supérieur à celui que nous avons adopté

A suivre avec un exemple concret

Retour page d'accueil