TURBINES ACTUELLES

Il ne saurait être question de traiter ici in extenso des turbines modernes. Notre étude s'intéresse aux roues . Nous ferons sur les turbines un rapide parcours. Les turbines ont fait l'objet de débuts, de recherches et d'études poussées .Les publications les décrivant dans le détail avec tous les calculs souhaités sont rares , les constructeurs par ailleurs cachent leurs secrets concernant notamment les tracés des aubes ; avec le temps , cependant ces secrets commencent à perdre de leur exclusivité.
Je ne connais que 2 ouvrages très complet sur cette question édité par Eyrolles mais introuvable .

Le premier  a été écrit vers 1935 par André Tenot , auteur par ailleurs d'une thèse de doctorat sur cette même question à l'université de Toulouse en 1934 .
Le second plus récent est de Louis Vivien .Il est également épuisé.

Ce qui a permis un progrès définitif, c ' est le développement de la mécanique des fluides et l'acquisition des notions de similitude.
La turbine est évidemment bien plus complexe que la roue.

Certes , on sait calculer les triangles des vitesses a l'entrée et à la sortie , mais le long d'une aube , c'est moins simple .

Le calcul tout le long de cette aube par les théorèmes d'Euler et de Bernoulli en mouvement relatif , conduisent à des équation dites aux dérivées partielles qu'on ne savait pas intégrer jusqu'à l'avènement des ordinateurs.

Cette roue de plus de 2 mètres de hauteur a été mise au point avec un modèle réduit de 200 mm

Grâce à eux , on a encore gagné quelques points sur le rendement qui déjà était élevé.
Car les tracés étaient empiriques en fait , et on était grandement secouru par les modèles réduits.
Pour comprendre à quoi pouvaient servir ces derniers , il faut passer par la notion de vitesse spécifique , notion qui elle n'est nullement dépassée , bien au contraire car on la retrouve partout en mécanique des fluides et en aérodynamique.

Avec la roue Pelton représentée sur la figure , on est dans le cas extrême ou toute l'énergie de l'eau passe par la voie cinétique. Les roues Pelton sont d'une espèce  à part .C'est le principe de la roue en dessous qui est ici poussé au maximum de ses possibilités : alors que la roue en dessous avait un rendement de l'ordre de 35% , celui de la roue de Malgovert dépasse 90% 

Ces turbines sont activées par l'intermédiaire d'un injecteur qui est un robinet sans pertes de charge et de haute précision.
Les autres roues sont les Francis et les hélices , dénommées Kaplan du nom de leur inventeur quand leurs pales sont orientables ce qui est un grand progrès.

ACTION OU REACTION

Si toute l'énergie de l'eau est convertie en énergie cinétique avant d'entrer dans la roue , la pression est nulle c.a.d. égale à la pression atmosphérique : la turbine est à ACTION : Cas des  Pelton
Si au contraire l'eau entre plus lentement dans la roue , la pression  à l'entrée des aubes sera forte mais il y aura une perte de pression en sortie de roue : la machine est à REACTION : cas des Francis et hélices
En gros on peut dire qu'en quittant la roue l'eau abandonne sa pression , ce qui provoque le couple moteur.
Mais il faut observer que l'eau est obligée de quitter la roue à une certaine vitesse
L'énergie correspondant à cette vitesse est provisoirement perdue

Intuitivement , cette notion de réaction est plus difficile à saisir pour les machines centripètes que pour les centrifuges (Turbine Fourneyron) mais la construction de ce dernier type a été abandonné après la découverte de la Francis qui est centripète.
Les Francis et les hélices ont certain degré de réaction qui dépend de leur tracé.
Pour plus de détails concernant ces question , voir la page réservée aux turbines à réction


La notion de vitesse de roue est généralement interprétée comme suit:
Roue lente :    Ns faible
Roue rapide  : Ns élevé
Cette notion n'est pas dans le sens ou on penserait pouvoir l'entendre :
Les roues lentes , en effet tournent généralement vite
Les roues rapides  tournent généralement lentement

Un exemple nous sera donné par une roue d'une centrale du Rhin (basse chute), Kembs par exemple (1932)
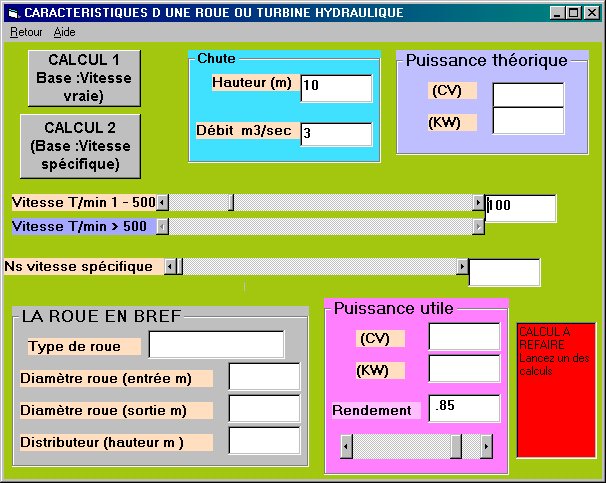
Dans cette usine une seule roue a une puissance de 33000 KW sous 15 mètres de chute et un débit de 230 m3/s .
Elle tourne à 93.75  t/min . Le Ns est de 650 .Son diamètre est de 6  mètres .
Les roues d'origine (hélices à pales fixes) ont été progressivement remplacées par des Kaplan.

Le dessin ci dessous nous montre une roue de ce type , de fabrication très récente et dont les dimensions sont du même ordre.
Le profil des pales est donné par des calculs hydrodynamiques qui s'apparentent à ceux des ailes d'avion , l'épaisseur doit tenir compte des efforts considérables qui s'exercent sur la pale entre l'intrados et l'extrados , compte tenu de la différence de pression entre ces 2 surfaces.
On est bien loin de la roue de moulin !!!

l

Dans le tableau ci dessous qui ne donne que des ordres de grandeur, les appellations pour la chute (haute , moyenne , ) sont toutes relatives .

(Les Pelton sont exclues de ce tableau étant donné comme déjà vu leur caractère particulier)

Toutes ces roues sont précédées d'un distributeur (vannage qui a pour but de régler le débit et d'orienter la direction de la vitesse de l'eau sans créer de perte de charge ) .



Pour cette raison les directrices du vannage sont profilées "comme des ailes d'avion"
En amont , l'arrivée d'eau est assurée par une bâche spirale ou bien la roue est noyée dans la chambre d'eau qui est le prolongement (et la fin) du canal d'amenée , le distributeur est alors généralement de forme conique .
   
La roue ci contre est incluse dans une bâche spirale , solution adoptée dès que la chute a une certaine

Les valeurs de Vc entrée % et Vc sortie % sont les vitesses circonférentielles en pourcentage de racine de (2*g*H)
Ainsi une roue de Ns 100 sous 200 mètres de chute aura une vitesse circonférentielle sur son bord d'entrée de 0.7 * racine de (2*g*200) soit 44 m/sec environ
Si elle tourne à 1000 t/min , nous en déduisons aussitôt le diamètre d'entrée: 0.85 mètres.
Le diamètre de sortie sera bien plus petit avec ce Ns .
En calculant à partir de la formule du Ns la puissance compatible nous trouvons une puissance de 5700 CV
On trouve un débit de 2.51 m3/s en admettant un rendement de 0.85
Ces résultats seront rapidement confirmés par mon logiciel de pré-calcul de roue (Version 4)

Voir le téléchargement

Présentation de ce logiciel pour l'exemple ci dessus (la version 4 que vous obtiendrez est nettement améliorée par rapport aux versions 2 et 3 , une mise à jour simple est possible)


Etudes du tracé
Le tracé des aubes ou pales se fait selon des méthodes complexes qui échappent à notre exposé 
Ci dessous un exemple qui montre comment les aubes d'une Francis étaient étudiées par des "turbines partielles" (coupes planes - ou cylindriques - dans la roue )

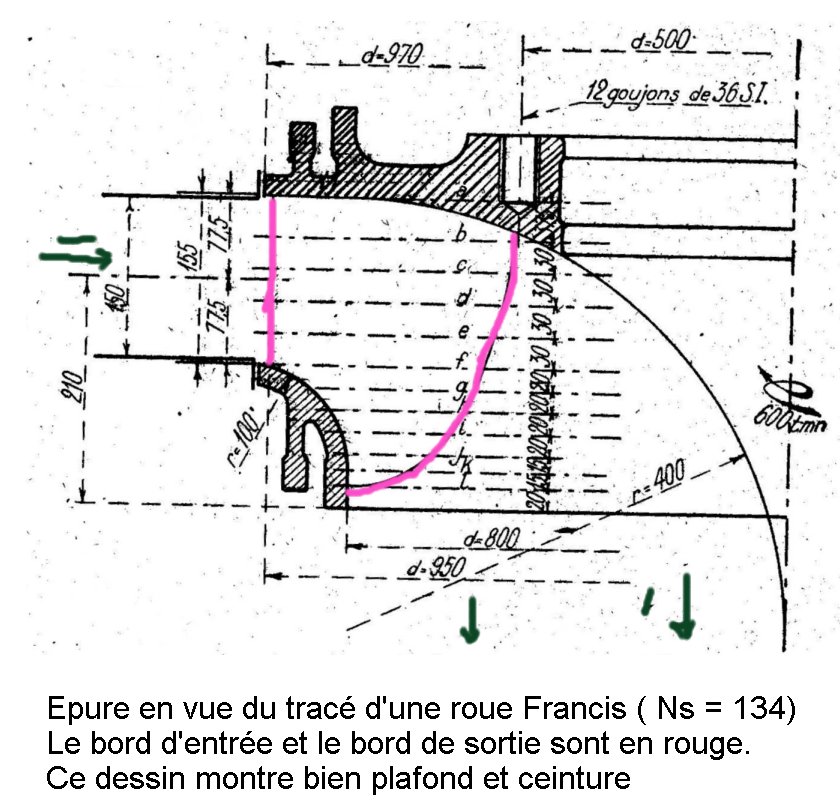
A la sortie de la roue l'eau n'est pas encore descendue au niveau du canal de fuite.
Elle est guidée vers ce canal par un tuyau aspirateur .
Celui ci permet de récupérer la hauteur qui semblerait perdue.
L'application du théorème de Bernoulli entre entre le haut et le bas de cet aspirateur donne la relation suivante :
ps + Hs  + v*v/(2*g) =patm +  0 + v*v/(2*g)
ps : pression de l'eau à la sortie de la roue

Hs  : hauteur de l'aspirateur

patm =pression atmosphérique =0 car toutes nos pressions snot calculées par rapport à la pression atmosphérique .

On en déduit ps =-Hs
Si la vitesse de sortie est élevée (hélices) il y a intérêt à récupérer cette vitesse en améliorant notre tuyau qui s'élargira progressivement selon une forme qui peut être très élaborée .
Le terme v*v/(2*g) est pratiquement nul car la vitesse finale est très faible.
L'équation ci dessus devient
ps + Hs  + v*v/(2*g) =0    et :
ps =-Hs -v*v/(2*g) 

La hauteur Hs a une limite théorique de 10. 33 m  pour éviter la création du vide et l'apparition de phénomènes de cavitation très nuisibles car ils provoquent unre érosion rapide du métal de la roue
En fait la limite de Hs  est  inférieure à 10. 33 m 
Cette limite est propre à chaque installation et dépend de divers facteurs sur lesquels je ne peux m'étendre ici sans rendre complexe la lecture du texte pour la majorité des lecteurs

POUSSEE  AXIALE

En traversant la roue , l'eau n'exerce pas seulement un couple moteur : elle exerce aussi une poussée dans le sens de la composante axiale de la vitesse à la sortie. 

Cette poussée , nuisible, oblige à munir la machine d 'un palier de butée (crapaudine) dont le graissage devra être surveillé et sa conception est très élaborée sur les grosses machines.

PARTICULARITES

En montant dos à dos sur le même arbres 2 turbines symétriques , on annule la poussée axiale , en doublant la puissance.
Cette formule suppose logiquement un axe horizontal

Dans le cas des Peltons , on peut augmenter le nombre d'injecteurs sur une même roue.
On ne dépasse pas généralement 3 injecteurs , mais on eut aller jusqu'à 6 .
La puissance est multipliée par le nombre d' injecteurs et la vitesse spécifique par la racine carrée de ce nombre .

GROUPES BULBES
Dans le cas des Kaplan l'eau est déviée à 90°

On a recherché des solutions plus 
audacieuses avec un écoulement axial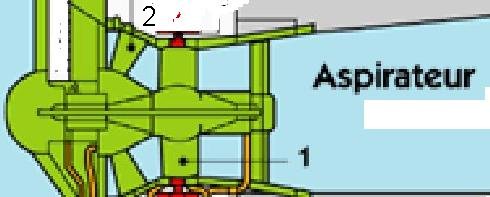 

Ce mode d'écoulement permet d'installer les machines 
"dans le lit de la rivière" supprimant ainsi le bâtiment d'usine
Il en résulte une disposition particulière du distributeur    
L'extrait ci joint d'une image montre la disposition adoptée
La roue est la pièce repérée 1

Les roues ont un Ns très élevé (1000 env. et plus)
Les directrices sont repérées 2
L'étude approfondie de ces machines dépasse le cadre de notre projet de site et n'est citée que pour mémoire



QUELQUES SITES SUR CES MACHINES

 Site on water turbines,   en anglais ce dernier donnant un bon coup d'oeil sur les différents types de roues


Nous vous proposons maintenant d'étudier une roue assez curieuse:

La turbine Banki